Trilateration is the method of locating points in space based on measuring the distances from known reference locations. It is used in surveying and navigation, similarly to the related method of triangulation, which technically uses the measurement of angles, not distances. For this entry we’re going to get practical and attempt to do some trilateration, using distances between some major cities in the world. To do this, I’ll need some equipment:

I acquired graph paper, a ruler, a tape measure, a pen, a pair of compasses, and a couple of large polystyrene balls.
I began my first scale drawing on a piece of graph paper. I’ve picked Auckland, New Zealand, as one of my cities of interest. Since nothing is on the paper yet, I can place Auckland wherever I want to. So I draw a cross indicating the position of Auckland and label it AKL (the city’s international airport code).

For my second city, I’ve chosen Tokyo, Japan. According to a flight distance reference website, the travelling distance between Auckland and Tokyo, or more specifically between Auckland Airport and Tokyo’s Narita Airport, is 8806 kilometres. My graph paper has 2 mm squares, and (for reasons that will become clear in a minute) I’m using a scale of 86.1 km/mm. So I take a pair of compasses and set the distance from the metal point to the pen tip to be 102.3 mm as best I can. That’s 51 and a bit grid squares. I place the point in the centre of the AKL cross and mark a point on the paper 102.3 mm away with the pen tip. I enlarge the point to a cross and label it NRT (for Narita Airport). It doesn’t matter which direction I choose to place Tokyo from Auckland, because at this point there are no other constraints.

For my third city, I choose Los Angeles, USA. Los Angeles Airport, LAX, is 10467 km from Auckland, and 8773 km from Tokyo Narita. To locate LAX on my scale drawing, I first set my compasses with a distance of 10467 / 86.1 = 121.6 mm. With this distance setting, I draw an arc centred on AKL.
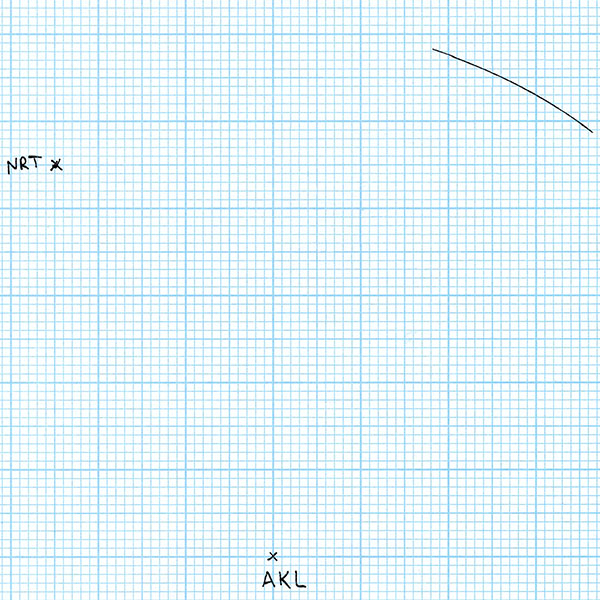
All of the points on this arc are the correct distance from Auckland to be Los Angeles. But we have another constraint – Los Angeles also has to be the correct distance from Tokyo. So I set my compasses to 8773 / 86.1 = 101.9 mm, and draw an arc centred at NRT.
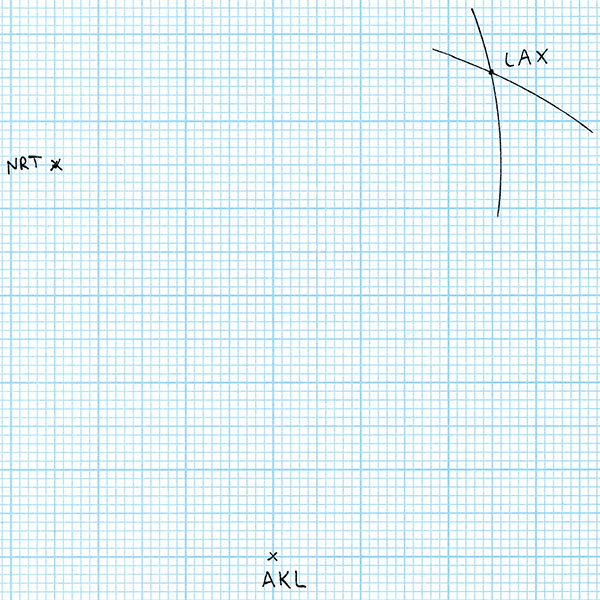
The intersection of these two arcs is the point that is both the correct scale distance from Auckland and Tokyo, so I label the intersection point LAX. So far, so good. We have three world cities with their relative positions accurately plotted to scale. Let’s add a fourth city! For the fourth city, I’ll choose something somewhere in the middle of the first three: Honolulu, USA. For starters, Honolulu is 7063 km from Auckland. So I draw an arc with radius 7063 / 86.1 = 82.0 mm centred on AKL.

Honolulu is 6146 km from Tokyo. So I draw an arc with radius 6146 / 86.1 = 71.4 mm centred on NRT.
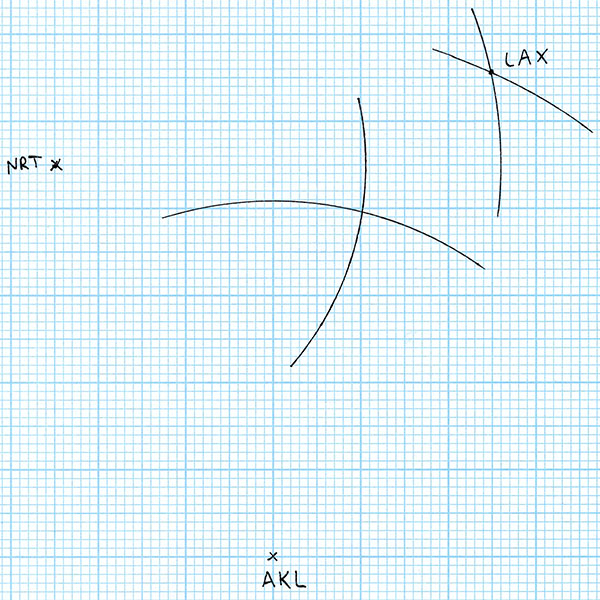
Now in theory this is enough to give us the location of Honululu. It must be on both the arc centred at Auckland and on the arc centred at Tokyo – so it has to be at the intersection of those two arcs. But wait! We have more information than that. We also know that Honolulu is 4113 km from Los Angeles. So I draw an arc with radius 4113 / 86.1 = 47.8 mm centred on LAX.
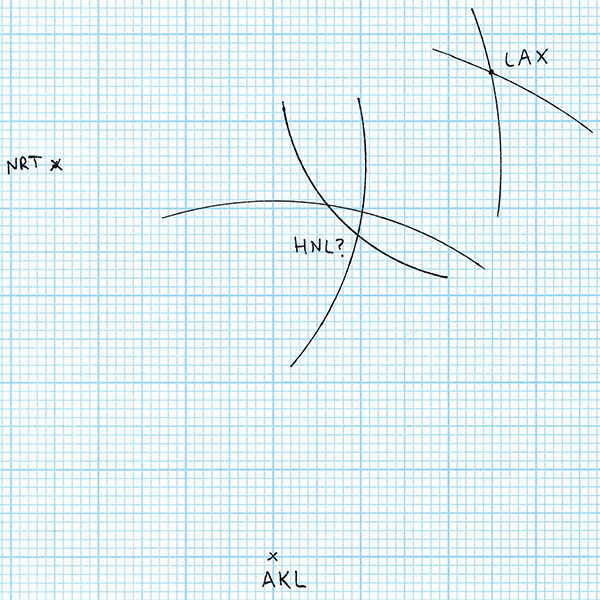
For the flight distances to be correct, Honolulu Airport (HNL) must be on all three arcs that I’ve drawn. But the arcs don’t all intersect at the same point. So where is Honolulu? According to the rules of geometry, anywhere we put it results in at least one of the distances being wrong. In the worst case, the the AKL-LAX intersection is 10 mm on the drawing from the NRT-LAX intersection, an error of 861 kilometres, which is 300 km longer than the entire chain of populated Hawaiian Islands from Niihau to Hawaii. Obviously a navigation error this large when trying to find Honolulu in the midst of the Pacific Ocean would be disastrous.
What’s gone wrong? Well, I’ve attempted to draw these distances to scale on a flat piece of paper. The error shows the distortion caused by trying to map the shape of the Earth onto a flat surface. The distances are all correct, but in reality they don’t lie in the same plane. So let’s try another approach. I’m going to map the distances onto a scale model of the Earth as a sphere.
To do this, I got a polystyrene sphere from an art supply shop. I measured the circumference using a tape measure to be 465 mm. Dividing the average circumference of the Earth by this gives me a scale of 86.1 km/mm (which is where I got the scale that I used for the drawing above). Now I just need to repeat the steps above, but plot the points and arcs on the surface of the sphere. But there’s one small wrinkle: flight distances are measured along the surface of the Earth, but the compasses step off the distance in a straight line, as measured through the Earth. To get the correct scale distance to set the compasses, we need to do a little geometry:
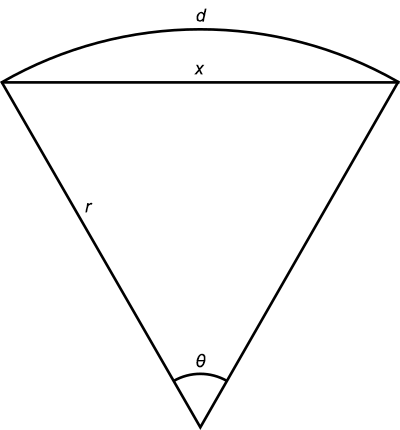
The distance along the surface of the Earth is d, the distance through the Earth is x, and the radius of the Earth is r. In radians, the angle θ is d/r. Now according to the cosine rule of trigonometry:
x2 = r2 + r2 – 2r2 cos θ
x2 = 2r2(1 – cos(d/r))
So plugging in d and r we can find the distance x to set the compasses to (at the correct scale). Here’s a summary table:
| Cities | Distance (km) | Scale distance (mm) | Compasses distance (mm) |
|---|---|---|---|
| AKL-NRT | 8806 | 102.3 | 94.3 |
| AKL-LAX | 10467 | 121.6 | 108.4 |
| NRT-LAX | 8773 | 102.0 | 94.0 |
| AKL-HNL | 7063 | 82.1 | 77.9 |
| NRT-HNL | 6146 | 71.4 | 68.6 |
| LAX-HNL | 4113 | 47.8 | 46.9 |
Using the distances in the Compasses column on my polystyrene sphere, and following the same steps as above for the graph paper, produced this:

The arcs drawn with the correct scale distances of Honolulu from Auckland, Tokyo, and Los Angeles all intersect at exactly the same point on the surface of the sphere. We’ve found Honolulu!
So by experiment, trilateration of points on the Earth’s surface does not work if you use a flat surface to map the points. It only works if you use a sphere.
Addendum: I bought two spheres because I was prepared for the first attempt to be a little bit out due to any small inaccuracies or mistakes in my setting the correct compasses distances. But as it turned out I only needed the one. I was pleasantly surprised when it worked so well the first time.