If you hold your arm outstretched before you with a finger raised in front of some object in the distance, and you close one eye and align your finger so that it looks directly in front of a particular object, then close that eye and open the other eye, then your finger will appear to have moved sideways. This is because your left eye and your right eye are not in the same position, so lining up your finger with an object using one eye means that it is not aligned with the other eye. This effect is known as parallax.
Parallax is a purely geometric effect, caused by the divergence of straight lines drawn from a common object to two different viewpoints. We make use of parallax unconsciously, our brains using the different visual information from our two eyes to give us the sensation of viewing a three dimensional world around us.
We’ve discusses parallax briefly in Proof 28: Stereo imaging. Here’s a repeat of the diagram illustrating parallax (with a dog instead of a finger).

Illustration of parallax. The dog is closer than the background scene. Sightlines from your left and right eyes passing through the dog project to different areas of the background. So the view seen by your left and right eyes show the dog in different positions relative to the background. (The effect is exaggerated here for clarity.)
Parallax can be observed wherever you look at two objects at different distances. If you measure the distance between the two viewpoints and the angle between the two different sightlines, and you know the distance to one of the objects, then by simple geometry you can calculate the distance to the other object. A handy approximation is that if one object is much further away than the near object, then you can assume it is infinitely far away, which simplifies the geometry and produces only a negligibly small error.
Parallax can be used in this way to measure the distance to some astronomical objects, namely those objects close enough to Earth to have a measurable parallax angle when compared to the positions of distant stars. This includes objects in our solar system, as well as the very nearest stars. The European Space Agency satellite Hipparcos measured parallaxes of around 100,000 stars, using observations made six months apart so that the two different viewpoints are on opposite sides of the Earth’s orbit, a viewpoint separation baseline of 300 million km. Even with this enormous baseline, the parallax angle of stars is less than one second of arc, requiring precise instruments to even detect. However, there is a much closer celestial object for which the parallax is readily visible with a smaller baseline: the moon.
The moon is not close enough to see parallax from your left and right eyes. It is however close enough that photos of the moon taken from different locations on the Earth at the same time show the moon significantly shifted against the background of stars. With viewpoints on opposite sides of the Earth, the parallax angle of the moon is about one degree – it varies slightly due to the moon’s elliptical orbit.
Illustration of parallax of the moon, as seen from four different points on the Earth’s surface at the same time. Viewed from the North Pole, the moon occults stars in the constellation of Pleiades, but viewed from other locations the moon does not occult the same stars. (Public domain image from Wikimedia Commons.)
Using such observations of the moon, and knowing how far apart the viewpoints are, you can calculate the distance to the moon with high accuracy. But you can also do the reverse calculation: if you know the distance to the moon, you can calculate how far apart the viewpoint locations are. As mentioned in Proof 32: Satellite laser ranging, we have an independent method of measuring the distance to the moon, to an accuracy of better than a millimetre, by bouncing lasers off reflectors left on the moon by the Apollo astronauts. Before 1969, we could also measure the distance to the moon using radar ranging, to an accuracy of about 1 km.[1][2]
Incidentally, the 1965 paper by Yaplee, et al.[2], also includes a calculation of the radius of the Earth from the radar ranging data, as it comes out as a variable that can be solved for if you know the acceleration due to gravity at Earth’s surface and the ratio of the Earth’s mass to the moon’s mass, which were known at the time. Given their radar results, the authors calculate the Earth’s equatorial radius to be 6378.167 km, only 30 metres different to the current reference value of 6378.137 km. (Obviously a result unobtainable if you assume the Earth is flat.)
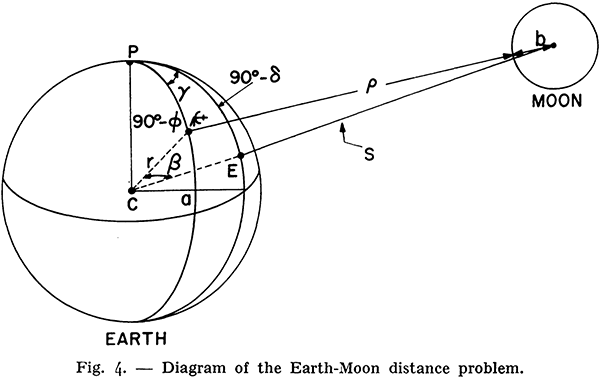
Diagram from Yaplee, et al., showing the geometry of the Earth-moon system for the purpose of determining the distance to the moon using radar ranging. (Figure reproduced from [2].)
So even without using parallax we know the distance to the moon. This means we can do the reverse calculation, and figure out how far apart different viewpoints (such as the North Pole and South Pole) are. Any two antipodal points, on opposite sides of the Earth, are about 20,000 km apart – as the crow flies, or as a traveller would have to cover to go from one point to the other. However if you calculate how far apart those points are using lunar parallax, you find that they are actually about 12,730 km apart. Why such a big discrepancy?
The simplest explanation for this is that the Earth’s surface is curved, with 20,000 km representing the semi-circumference and 12,730 km being the diameter (twice the radius) of curvature. If the Earth were flat, then the calculated distance between two points for which the travel distance is 20,000 km would also have to be 20,000 km.
Experiment:
With your help, we can perform a lunar parallax experiment to see if the Earth is flat or not, and to measure its radius if we assume it’s spherical. All we need to do is take some photos of the moon and the background stars at the same time, from different places around the world. The best time to do this is when the moon is up most of the night, which means a full moon. The next full moon after this is published occurs on 31 October 2020 at 14:49 UTC. This means the night of 31 October-1 November is perhaps the best time to do this. However I will be travelling that night and unable to participate myself, and perhaps many people will be busy with Halloween activities. So I propose we do it on the following night: the evening of 1 November into the morning of 2 November. This has the slight advantage that the moon rises and sets a bit later, meaning it will be easier for people to get a photo just before sunrise, which is vitally important as I shall explain.
I could set one specific time for everyone to take photos, but that would not be ideal, because half the planet won’t be able to see the moon at the given time, and there will also be places where the moon is up, but it will be too light to see stars. So instead, we will take photos on the hour, every hour, for as much of the night as you can manage. For this to provide useful data, the photos must satisfy the following conditions:
1. We absolutely must have some photos taken in the midnight-to-sunrise period, and preferably some taken just before sunrise (e.g. 4 or 5 a.m.). This is so they can be matched with photos taken in the evening in different time zones. If everyone just takes a few photos in the evening and goes to bed, this won’t work. It’s better if you take a shot before going to bed, and then drag yourself out of bed for another shot before sunrise. I realise not everybody will want to do this, but at least some of you will need to. If you really can’t manage it, please stay up as late as possible and shoot every hour until you do go to bed.
2. Stars must be visible in the photos. Enough stars that we can recognise the constellations, not just 3 or 4 stars. This means you will need to overexpose the moon quite severely. That’s fine, we’re not interested in seeing details of the moon, as long as we can figure out where the middle of the moon is. This means you shouldn’t zoom right into the moon – a moderate focal length lens will work fine, around 50-100 mm for a 35 mm camera. Go out some night beforehand and practice taking a photo of stars to figure out the correct exposure.
Some example photos that would be fine for this experiment:
- https://www.flickr.com/photos/buwaneka/20062415890/
- https://www.flickr.com/photos/maxwallefeld/21597236419/
- https://www.flickr.com/photos/pauls_photo_stuff/29627007132/
If you’re interested in taking photos for this experiment, please contact me (dmm [at] dangermouse.net) to register your interest, with your location and a list of hours that you would be willing to be awake to take photos. Maybe send me a sample photo you’ve taken showing stars. I’ll coordinate the list and make sure we have enough people to make the experiment worthwhile, and will let everyone know a few days beforehand whether we will go ahead, or if we should postpone the date until we get more people. And if we do go ahead, what hours will be most valuable for you to take photos.
References:
[1] Yaplee, B. S., Bruton, R. H., Craig, K. J., Roman., N. G. “Radar echoes from the moon at a wavelength of 10 cm.” Proceedings of the Institute of Radio Engineers, 46(1), p. 293-297, 1958. https://doi.org/10.1109/JRPROC.1958.286790
[2] Yaplee, B. S., Knowles, S. H., Shapiro, A., Craig, K. J., Brouwer, D. “The mean distance to the Moon as determined by radar.” In Symposium-International Astronomical Union, 21, p. 81-93, Cambridge University Press, 1965. https://doi.org/10.1017/S0074180900104826
