The earliest method of marking time during the day was by following the movements of the sun as it crossed the sky, from sunrise in the east to sunset in the west. The apparent motion of the sun makes the shadows of fixed objects move during the day too. If you poke a stick into the ground, the shadow of the stick moves across the ground as time passes. By making marks on the ground and seeing which one the shadow is near, you get a method of telling the time of day. This is a simple form of sundial.
The apparent motion of the sun in the sky is caused by the interaction between the Earth’s orbit around the sun and the rotation of the Earth on its axis, which is inclined at approximately 23.5° to the axis of the orbital plane. At the June solstice (roughly 21 June), the northern hemisphere is maximally pointed towards the sun, making it summer while the southern hemisphere has winter. Half a year later at the December solstice, the sun is on the other side of the Earth, making it summer in the south and winter in the north. Midway between the solstices, at the March and September equinoxes, both hemispheres receive the same amount of sun.
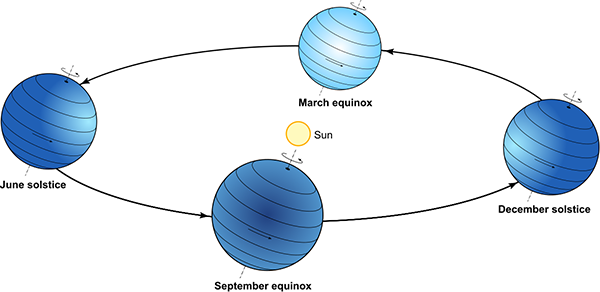
Diagram of the interaction between Earth’s orbit and its tilted axis of rotation, showing the solstices and equinoxes that generate the seasons.
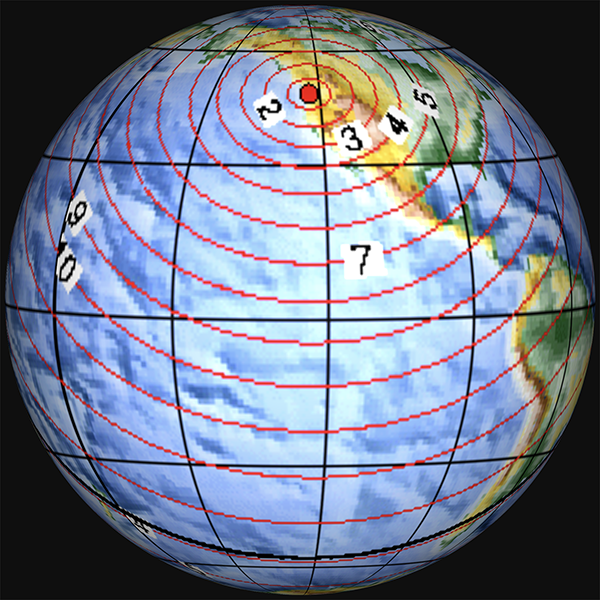
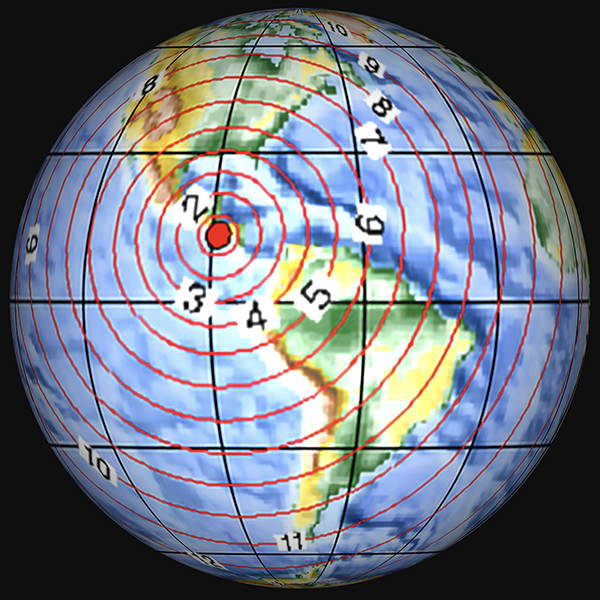
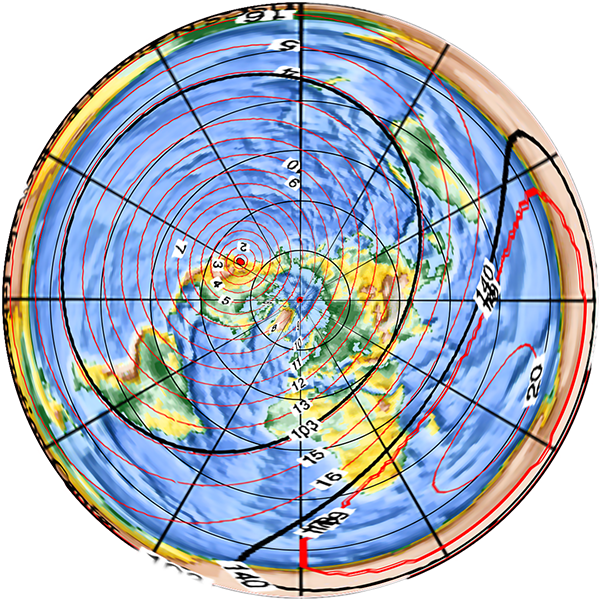
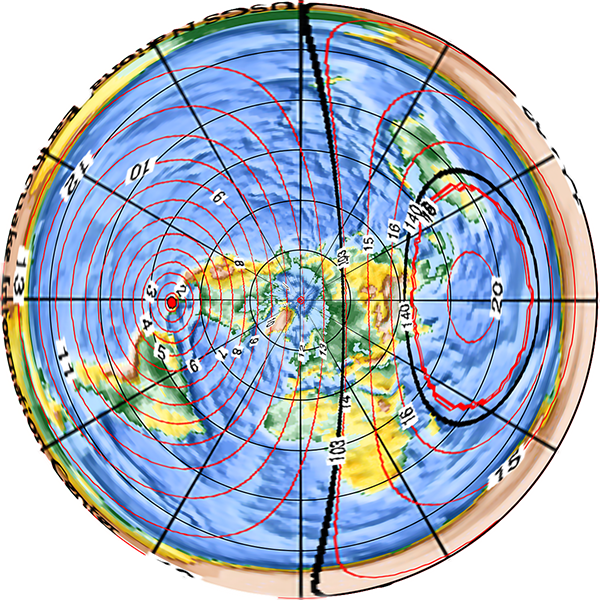
From the point of view of an observer standing on the Earth’s surface, the motions of the Earth make it appear as though the sun moves across the sky once per day, and drifts slowly north and south throughout the year. The following diagram shows the path of the sun across the sky for different dates, for my home of Sydney (latitude 34°S).
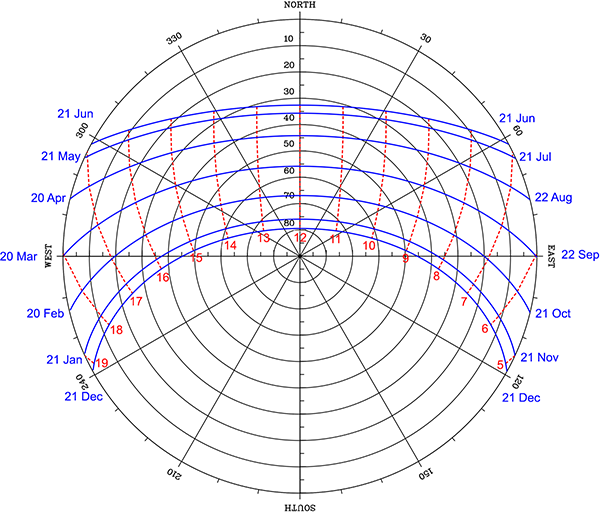
Sun’s path across the sky for different dates at latitude 34°S. (Diagram produced using [1].)
In the diagram, the horizon is around the edge, and the centre of the circles is directly overhead. The blue lines show the sun’s path for the indicated dates of the year. The sun is lowest in the sky to the north, and visible for the shortest time, on the June solstice (the southern winter), while it is highest in the sky and visible for the longest on the December solstice (in summer). The red lines show the position of the sun along each arc at the labelled hour of the day. For a location in the northern hemisphere north of the tropics, the sun paths would be curved the other way, passing south of overhead. In the tropics (between the Tropics of Capricorn and Cancer), some paths are to the north while some are to the south. On the equinoxes (20 March and 21 September), the sun rises due east at 06:00 and sets due west at 18:00 – this is true for every latitude.
If you have a fixed object cast a shadow, that shadow moves throughout the course of a day. The next day, if the sun has moved north or south because of the slowly changing seasons, the path the shadow traces moves a little bit above or below the previous day’s path.
The ancient Babylonians and Egyptians used sundials, and the ancient Greeks used their knowledge of geometry to develop several different styles. Greek sundials typically used a point-like object, called the nodus, as the reference marker. The nodus could be the very tip of a stick, a small ball or disc supported by thin wires, or a small hole that lets a spot of sunlight through. The shadow of the nodus (or the spot of light in the case of a hole nodus) moves across a surface in a regular way, not just with time of day, but also with the day of the year. During the day, the point-like shadow of a nodus traces a path from west to east (as the sun moves east to west in the sky). Throughout the year, the daily path moves north and south as the sun moves further south or north in the sky due to the seasons.

A nodus-based sundial, on St. Mary’s Basilica, Kraków, Poland. The nodus is a small hole in the centre of the cross. The horizontal position of the spot of light in the centre of the cross’s shadow indicates a time of just after 1:45 pm; the vertical position indicates the date (as indicated by the astrological symbols on the sides). It could be either about 1/3 of the way into the sign of Gemini (about 31 May), or 2/3 of the way through Cancer (about 12 July). The EXIF data on the photo indicates it was taken on 16 July, so the nodus date is fairly accurate. This sundial is mounted on a vertical wall, not horizontally, so the shadow travels left to right in the northern hemisphere, rather than right to left as it does for a horizontal sundial. (
Public domain image from Wikimedia Commons.)
There are two slight complications. The red lines in the sun’s path diagram show timing of the sun paths assuming the Earth’s orbit is perfectly circular, but in reality it is an ellipse, with the Earth nearest the sun in January and furthest away in June. Earth travels around that elliptical path at different speeds—due to Newton’s law of gravity and laws of motion—moving fastest at closest approach in January, and slowest in June. The result of this is that the daily interval between when the sun crosses the north-south line is 24 hours on average, but varies systematically through the year. This variation in the sun’s apparent motion has a period of one year.
The second complication occurs because of the tilt of the Earth’s axis to the ecliptic plane in which it orbits. The sun’s apparent movement in the sky is due west (parallel to the Earth’s equator) only at the equinoxes. On any other date it moves at an angle, with a component of motion north or south, as it moves up or down the sky with the seasons. This north-south motion is maximal at the solstices. So at the solstices the westward component of the sun’s motion is less than it is at the equinoxes, meaning that it appears to move westward across the sky more slowly (because part of its speed is being used to move north or south). This variation in the sun’s apparent motion has a period of half a year.
To get the total variation in the sun’s motion, we need to add these two components. Doing so gives us the equation of time. This is the amount of time by which the sun’s position varies from the ideal “circular orbit, non-inclined axial spin” case, as a function of the day of the year.
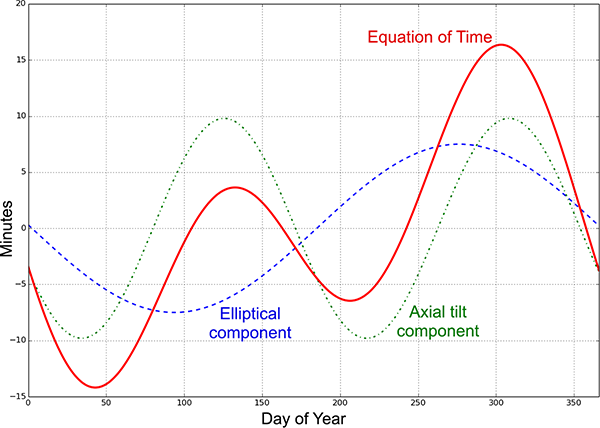
The equation of time (red), showing the two components that make it up: the component due to Earth’s elliptical orbit (blue dashed line) and the component caused by the Earth’s axial tilt (green dot-dash line). The total shows the number of minutes that the sun’s apparent motion is ahead of its average position.
What this means is that if you have a standard sort of simple sundial, the shadow moves at different speeds across the face on different dates of the year, resulting in the shadow getting a little bit ahead or a little bit behind clock time. To get the correct time as shown by a clock, you need to read the time off the sundial’s shadow and subtract the number of minutes given by the equation of time for that date.
But this is thinking about sundials with our modern mindest about how time works. We have decided to make the unit of time we call a “day” the average length of time that it takes the sun to return to its highest position in the sky, and then we’ve divided that day into 24 exactly equal hours. An hour on 20 March is exactly the same length as an hour on 21 June, or on 21 December. “Of course it is!” you say.
But it wasn’t always so. For most of history, a “day” was defined as either the time between one sunrise and the next, or one sunset and the next, or the time between when the sun was due south in the sky and when it returned to being due south again (in the northern hemisphere). Each of these definitions of a “day” vary in length throughout the year. Saudi Arabia officially used Arabic time up until 1968, which defined midnight (the start of a new day) to be at sunset each day, and clocks needed to be adjusted every day to track the shift in sunset through the seasons.
The definition of a day as the period between the sun being due south (or north) and returning to that position the next day, is called solar time. For most of human timekeeping history, this is what was used. The fact that some days were a bit longer or shorter than others was of no consequence when the sun itself was the best timekeeping tool that anyone had access to.
Our modern concept of an hour has its origins in ancient Egypt, around 2,500 BC. The Egyptians originally divided the night time period into 12 parts, marked by the rising of particular stars in the sky. Because the stars change with the seasons (as discussed in 36. The visible stars), they had tables of which stars marked which hours for different dates of the year. Because of precession of the Earth’s orbit, the stars fell out of synch with the tables over the course of several centuries.
The oldest non-sundial timekeeping device that still exists is a water clock dating from the reign of Amenhotep III, around 1350 BC. It was a conical bowl, which was filled with water at sunset, and had a small outflow drip hole that let water out at a roughly constant rate. Inside the bowl is a set of 12 level marks, showing the water level at each of the 12 divisions of the night. But not just one set of 12 marks – there are multiple sets of 12 markings, with different spacings, that show the passage of the night time hours for different months of the year, when the length of the night is different.

Ancient Egyptian water clock (not Amenhotep’s one mentioned in the text). Dating uncertain, but possibly a much later Roman-era piece (circa 30 BC). The lower panel shows an unrolled cast of the interior of the conical bowl, showing the 12 different vertical rows of 12 differently spaced holes, indicating variable length hours for different months of the year. (Figure reproduced from [2].)
The oldest sundial we have is also from ancient Egypt, dating from around 1500 BC, a piece of limestone with a hole bored in it for a stick, and shadow marks, 12 of them, for dividing the daylight hours into 12 parts.

Ancient Egyptian sundial, circa 1500 BC, found in the Valley of the Kings. (
Public domain image from Wikimedia Commons.)
So the ancient Egyptians were dividing both the daylight and night time parts of each day into 12 different-length parts for a total of 24 divisions. Through cultural contact, sundials became a common way to mark the 12 hours of daylight in many other Mediterranean and Middle Eastern civilisations too, including the ancient Greeks and Romans.
By the Middle Ages, Catholic Europe was still keeping time based on a division of daylight time into 12 variable-length hours, and this carried across to the canonical hours, marking the times of day for liturgical prayers:
- Matins: the night time prayer, recited some time after midnight, but before dawn.
- Lauds: the dawn prayer, taking place at first light.
- Prime: recited during the first hour of daylight.
- Terce: at the third hour of the day time.
- Sext: at midday, at the sixth hour, when the sun is due south.
- Nones: the ninth hour of the day time.
- Vespers: the sunset prayer, at the twelfth hour of the daylight period.
- Compline: the end of the working day prayer, just before bed time.
In the modern world we might interpret “the third hour” to be 9:00 am, halfway between 6:00 am and midday, but the canonical hours are guided by the sun, so Terce would be earlier in summer and later in winter, in the same way that sunrise, and hence the celebration of Lauds, are. Nones, in contrast, would be earlier in winter and later in summer. (Incidentally, we get our modern word “noon” from “Nones” – although you’ll notice that Nones was defined as the ninth hour, or around 3:00 pm. For some reason it moved to become associated with the middle of the day. We’re not sure exactly why, but historians believe that the monks who observed this liturgy fasted each day until after the prayer of Nones, so there was constant pressure to make it slightly earlier, which eventually moved it back a full three hours!)
You might think that when mechanical clocks were invented, people suddenly realised that they’d been doing things wrong the whole time, and they quickly moved to the modern system of an hour being of a constant length. But that’s not what happened. The first mechanical clocks used a verge escapement to regulate the motion of the gear wheels, and this remained the most accurate clock mechanism from the 13th century to the 17th. But it wasn’t very accurate, varying by around 15 minutes per day, and so verge clocks had to be reset daily to match the motion of the sun.

Verge escapement clock at Salisbury Cathedral (circa 1386). (My photo.)
Christiaan Huygens invented the pendulum clock in 1656, vastly improving the accuracy of mechanical clocks, down to around 15 seconds per day. With this new level of accuracy, people fully realised for the first time that the length of a full day as measured by the time it took the sun to return to the highest position in the sky didn’t match a regularly ticking clock. But rather than adjust their definition of what an hour was, people decided there must be a way to get these regular clocks to tell proper solar time! Thus were invented equation clocks.
The first equation clocks had a correction dial, which essentially displayed the equation of time value for the current day of the year. You read the time off the main clock dial, and then added the correction displayed on the correction dial, and that gave you the “correct” solar time. By the 18th century, the correction gearing was incorporated into the main clock face display, so that the hands of the clock actually ran faster or slower at different times of the year, to match the movement of the sun. It wasn’t until the early 19th century that European society moved to a mean time system (“mean” as in “average”), in which each “day” was defined to be exactly the same length, and the hour was a fixed period of time (thus simplifying clockmakers’ lives considerably).
Just to complete this story, clocks in the early 19th century were set to local mean time, which was the mean time of their meridian of longitude. Towns a few tens of miles east or west would have different mean times by a few minutes. This caused problems beginning with the introduction of rapid travel enabled by the railways, eventually leading to the adoption of standard time zones in the 1880s, in which all locations in slices of roughly 1/24 of the Earth share the same time.
What this means is that people were still living their lives by local solar time up until the early 19th century. In other words, a sundial was still the most accurate method of telling the time up until just 200 years ago – and it didn’t need any corrections based on the equation of time because people weren’t using mean time yet. It’s only in the past 200 years that we’ve had to correct a sundial to give what we consider to be the correct clock time.
So, back to sundials. Assuming we are happy with solar time (and can use the equation of time to correct to mean time if we wish), the main thing we need to contend with is that the sun moves north and south in the sky throughout the year. A nodus-type sundial accounts for this by marking lines that indicate the time when the shadow of the nodus crosses them on different days of the year. But many sundials use the whole edge of a stick or post as the shadow marker – this edge is called the gnomon. As the sun moves north and south throughout the year, different parts of the gnomon will cast their shadows in different places. If the gnomon is aligned parallel to the axis of the Earth, then these motions will be along the edge of the shadow, rather shifting the edge of the shadow laterally. You can then read solar time using a single marking, at any time of the year.
Another way to think about it is that from a viewpoint on Earth, the sun appears to revolve in the sky about the Earth’s axis. So if your sundial has a gnomon that is parallel to the Earth’s axis, the sun appears to rotate with the gnomon as its axis once per day, and the shadow of the gnomon indicates solar time on the marked surface below. As the sun moves north or south with the seasons, it is still revolving around the gnomon, so the shadow still tracks solar time accurately. If the gnomon is not parallel to the revolution axis, then as the sun moves north and south, the shadow of the gnomon will shift positions on the marked surface, and the time will be inaccurate at different times of the year.
This is why sundials with gnomons all have them inclined at an angle from the horizontal equal to the latitude of where the sundial is placed. At the North Pole, a vertical stick will indicate solar time accurately throughout the entire summer (when the sun is above the horizon 24 hours a day). At London (latitude 51.5°N), sundial gnomons are pointed north at 51.5° from the horizontal.

At Perth, Australia (32°S), they point south and are 32° from the horizontal, noticeably flatter.

A sundial in Perth, Australia. The gnomon is noticeably at a flatter angle than sundials in London. (
Public domain image from Wikimedia Commons.)
A sundial on the equator must have a gnomon that is horizontal.

A sundial in Singapore (latitude 1.3°N). The gnomon is the thin bar, angled at 1.3° to the horizontal. North is to the left. The sun shines from the north in June, from the south in December, but the shadow of the bar tracks the hours on the semicircular scale correctly at each date. (
Creative Commons Attribution 2.0 Generic image by Michael Coghlan, from Wikimedia Commons.)
So, in order to work properly, gnomon-sundials must have a gnomon angled parallel to the Earth’s axis of rotation. The fact that sundials at different latitudes need to have their gnomons at different angles to the ground plane shows that the ground plane is only perpendicular to the Earth’s rotation axis at the North and South Poles, and the angle between the ground and Earth’s axis of rotation varies everywhere else in a way consistent with the Earth being a globe.
If the Earth were flat… well, all of this would just be a huge coincidence in the motion of the sun above the flat Earth, that for some unexplained reason exactly mimics the geometry of a spherical Earth in orbit about the sun. In fact, to get all of the angles to match sundial observations you need to posit that the sun’s rays don’t even travel in straight lines.
Addendum: I just wanted to show you this magnificent sundial, in the Monastery of Lluc, in Mallorca, Spain.
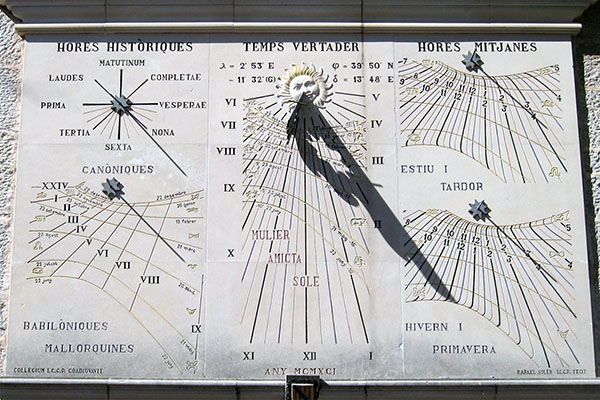
This sundial has five separate faces:
Top left shows the canonical hours. At sunrise (no matter what time sunrise happens to be), the shadow of the stick indicates the liturgy of Prime. Sext occurs at solar noon, when the sun is directly overhead, with Terce halfway between Prime and Sext. Vespers is at sunset (again, regardless of the modern clock time), with Nones halfway between Sext and Vespers. The night time hours of Complice, Matins, and Lauds are marked above the horizontal (and in fact would correctly indicate the times if the Earth were transparent, so the sun could cast a shadow from underneath the horizon).
Bottom left shows a nodus sundial, the tip of the stick marking “Babylonian” hours, which were used in Mallorca historically. This counts 0 (or 24) at sunrise, and then equal numbered hours thereafter. The vertical position of the nodus shadow marks the date (similar to the Krakow sundial above).
The central dial is a gnomon indicating “true solar time”. The shadow of the edge of the gnomon indicates the solar hour.
Finally the two dials on the right are nodus dials, showing mean time horizontally, and date of the year vertically. The top dial is to be read in summer and autumn, whole the lower dial is for winter and spring. It looks like the dials also include a daylight saving adjustment, assuming it begins and ends on the equinoxes!
The time (confirmed from the photo EXIF data) is 4:15 pm, and the date is 9 September, 12 days before the autumnal equinox (read on the top right dial).
References:
[1] “Polar sun path chart program”, University of Oregon Solar Radiation Monitoring Laboratory. http://solardat.uoregon.edu/PolarSunChartProgram.html
[2] Ritner, Robert. “Oriental Institute Museum Notes 16: Two Egyptian Clepsydrae (OIM E16875 and A7125)”. Journal of Near Eastern Studies, 75, p. 361-389, 2016. https://doi.org/10.1086/687296