special relativity – 100 Proofs that the Earth is a Globe

29. Neutrino beams

We’ve met neutrinos before, when talking about supernova 1987A.

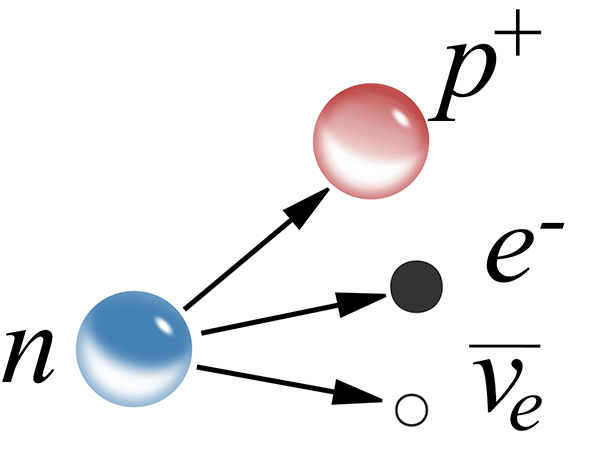
Historically, the early quantum physicist Wolfgang Pauli first proposed the existence of the neutrino in 1930, to explain a problem with then-current understanding of radioactive beta decay. In beta decay, an atomic nucleus emits an electron, which has a negative electric charge, and the resulting nucleus increases in positive charge, transmuting into the element with the next highest atomic number. The law of conservation of energy applied to this nuclear reaction implied that the electron should be emitted from any given isotope with a specific energy, balancing the change in mass as given by Einstein’s famous E = mc² (energy equals mass times the speed of light squared). Alpha particles emitted during alpha decay, and gamma rays emitted during gamma decay appear at fixed energies.

Illustration of beta decay. The nucleus at left emits an electron. (Public domain image from Wikimedia Commons.)

However, this was not what was observed for beta decay electrons. The ejected electrons had a maximum energy as predicted, but also appeared with a spread of lower energies. Pauli suggested that another particle was involved in the beta decay reaction, which carried off some of the energy. In a three-body reaction, the energy could be split between the electron and the new particle in a continuous fashion, thus explaining the spread of electron energies. Pauli suggested the new particle must be very light, so as to evade detection up to that time. He called it a “neutron”, a neutral particle following the word-ending convention of electron and proton.

However, in the same year German physicists Walther Bothe and Herbert Becker produced some strange radiation by bombarding light elements with alpha particles from radioactive polonium. This radiation had properties unlike other forms known at the time, and several experimenters tried to understand it. In 1932, James Chadwick performed experiments that demonstrated the radiation was made of neutral particles of about the same mass as a proton. The name “neutron” had been floating around nuclear physics for some time (Pauli wasn’t the first to use it; “neutron” appears in the literature as a name for proposed hypothetical neutral particles as early as 1899), but Chadwick was the first experimenter to demonstrate the existence of a neutral particle, so the name got attached to his discovery. Italian physicist Enrico Fermi responded by referring to Pauli’s proposed very light neutral particle as a “neutrino”, or “little neutron” in Italian coinage.

Beta decay. A neutron decays to produce a proton, an electron, and an electron anti-neutrino. The neutrino produced has to be an antiparticle to maintain matter/antimatter balance, though it is often referred to simply as a “neutrino” rather than an anti-neutrino. (Public domain image from Wikimedia Commons.)

Detection of the neutrino had to wait until 1956, when a sensitive enough experiment could be performed, by American physicists Clyde Cowan and Frederick Reines, for which Reines received the 1995 Nobel Prize in Physics (Cowan had unfortunately died in 1974). In 1962, Leon Lederman, Melvin Schwartz, and Jack Steinberger of Fermilab discovered that muons—particles similar to electrons but with more mass—had their own associated neutrinos, distinct from electron neutrinos. They received the Nobel Prize for this discovery in 1988 (only a 26 year wait, unlike Reines’ 39 year wait). Finally, Martin Perl discovered a third, even more massive electron-like particle, named the tau lepton, in 1975, for which he shared that 1995 Prize with Reines. The tau lepton, like the electron and muon, has its own distinct associated neutrino.

Meanwhile, other researchers had been building neutrino detectors to observe neutrinos emitted by the sun’s nuclear reactions. Neutrinos interact only extremely weakly with matter, so although approximately 7×10¹⁴ solar neutrinos hit every square metre of Earth every second, almost none of them affect anything, and in fact almost all of them pass straight through the Earth and continue into space without stopping. To detect neutrinos you need a large volume of transparent material; water is usually used. Occasionally one neutrino of the trillions that pass through every second will interact, causing a single-atom nuclear reaction that produces a brief flash of light, which can then be seen by light detectors positioned around the periphery of the transparent material.

Interior of the Daya Bay Reactor neutrino detector, China. The glassy bubbles house photodetectors to detect the flashes of light produced by neutrino interactions in the liquid filled interior (not filled in this photo). (Public domain image by U.S. Department of Energy, from Wikimedia Commons.)

When various solar neutrino detectors were turned on, there was a problem. They detected only about one third to one half of the number of neutrinos expected from models of how the sun works. The physics was thought to be well understood, so there was great trouble trying to reconcile the observations with theory. One of the least “break everything else we know about nuclear physics” proposals was that perhaps neutrinos could spontaneously and randomly change flavour, converting between electron, muon, and tau neutrinos. The neutrino detectors could only detect electron neutrinos, so if the neutrinos generated by the sun could change flavour (a process known as neutrino oscillation) during the time it took them to arrive at Earth, the result would be a roughly equal mix of the three flavours, so the detectors would only see about a third of them.

Another unanswered question about neutrinos was whether they had mass or not. Neutrinos have only ever been detected travelling at speeds so close to the speed of light that we weren’t sure if they were travelling at the speed of light (in which case they must be massless, like photons) or just a tiny fraction below it (in which case they must have a non-zero mass). Even the neutrinos detected from supernova 1987A, 168,000 light years away, arrived before the initial light pulse from the explosion (because the neutrinos passed immediately out of the star’s core, while the light had to contend with thousands of kilometres of opaque gas before being released), so we weren’t sure if they were travelling at the speed of light or just very close to it. Interestingly, the mass of neutrinos is tied to whether they can change flavour: if neutrinos are massless, then they can’t change flavour, whereas if they have mass, then they must be able to change flavour.

To test these properties, particle physicists began performing experiments to see if neutrinos could change flavour. To do this, you need to produce some neutrinos and then measure them a bit later to see if you can detect any that have changed flavour. But because neutrinos move at very close to the speed of light, you can’t detect them at the same place you create them; you need to have your detector a long way away. Preferably hundreds of kilometres or more.

The first such experiment was the KEK to Kamioka, or K2K experiment, running from 1999-2004. This involved the Japanese KEK laboratory in Tsukuba generating a beam of muon neutrinos and aiming the beam at the Super-Kamiokande neutrino detector at Kamioka, a distance of 250 kilometres away.

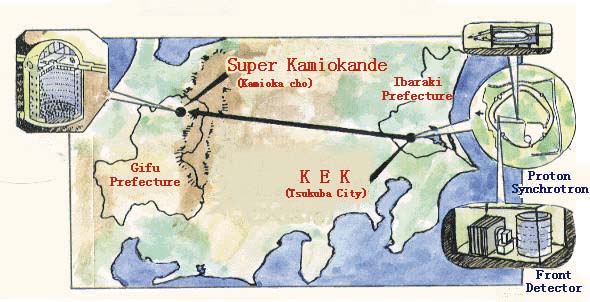
K2K map

Map of central Japan, showing the locations of KEK and Super-Kamiokande. (Figure reproduced from [1].)

The map is from the official website of KEK. Notice that Super-Kamiokande is on the other side of a mountain range from KEK. But this doesn’t matter, because neutrinos travel straight through solid matter! Interestingly, here’s another view of the neutrino path from the KEK website:

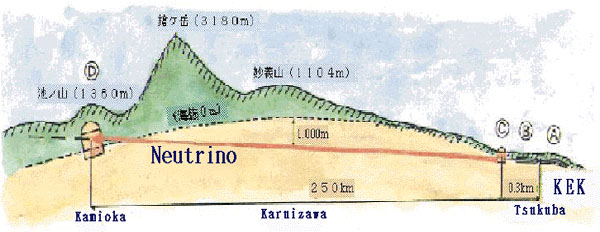
K2K cross section

Cross sectional view of neutrino beam path from KEK to Super-Kamiokande. (Figure reproduced from [1].)

You can see that the neutrino beam passes underneath the mountains from KEK to the underground location of the Super-Kamiokande detector, in a mine 1000 metres below Mount Ikeno (altitude 1360 m). KEK at Tsukuba is at an altitude of 35 m. Now because of the curvature of the Earth, the neutrino beam passes in a straight line 1000 m below sea level at its middle point. With the radius of the Earth 6367 km, Pythagoras’ theorem tells us that the centre of the beam path is 6365.8 km from the centre of the Earth, so 1200 m below the mean altitude of KEK and Super-Kamiokande – the maths works out. Importantly, the neutrino beam cannot be fired horizontally, it has to be aimed at an angle of about 0.5° into the ground for it to emerge correctly at Super-Kamiokande.

The K2K experiment succeeded in detecting a loss of muon neutrinos, establishing that some of them were oscillating into other neutrino flavours.

A follow up experiment, MINOS, began in 2005, this time using a neutrino beam generated at Fermilab in Illinois, firing at a detector located in the Soudan Mine in Minnesota, some 735 km away.

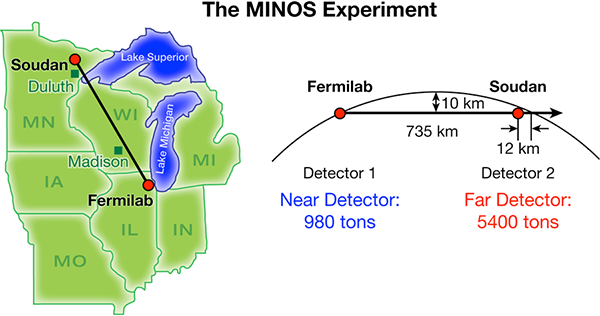
MINOS map and cross section

Map and sectional view of the MINOS experiment. (Figure reproduced from [2].)

In this case, the straight line neutrino path passes 10 km below the surface of the Earth, requiring the beam to be aimed downwards at an angle of 1.6° in order to successfully reach the detector. Another thing that MINOS did was to measure the time of flight of the neutrino beam between Fermilab and Soudan. When they sent a pulsed beam and measured the time taken for the pulse to arrive at Soudan, then divided it by the distance, they concluded that the speed of the neutrinos was between 0.999976 and 1.000126 times the speed of light, which is consistent with them not violating special relativity by exceeding the speed of light[3].

If you measure the distance from Fermilab to Soudan along the curvature of the Earth, as you would do for normal means of travel (or if the Earth were flat), you get a distance about 410 metres (or 0.06%) longer than the straight line distance through the Earth that the neutrinos took. If the scientists had used that distance, then their neutrino speed measurements would have given values 0.06% higher: 1.00053 to 1.00068 times the speed of light. In other words, to get a result that doesn’t violate known laws of physics, you have to take account of the fact that the Earth is spherical, and not flat.

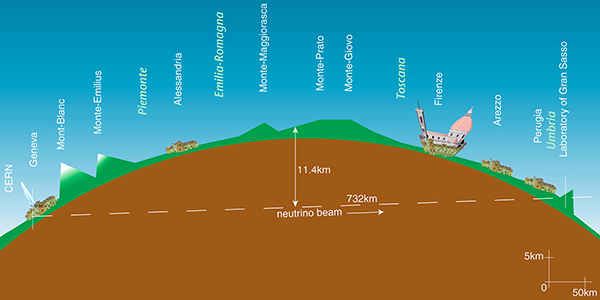
This result has been reproduced with reduced uncertainty bounds by the CERN Neutrinos to Gran Sasso (CNGS) experiment in Europe, which fires a neutrino beam from CERN in Switzerland to the OPERA detector at the Gran Sasso National Laboratory in Italy.

Sectional view of the CNGS experiment neutrino beam path. (Image is Copyright CERN, used under CERN Terms of Use, from [4].)

The difference between the neutrino travel times and the speed of light over the 732 km beam path was measured to be -1.9±3.7 nanoseconds, consistent with zero difference[5]. In this case, if a flat Earth model had been used, the beam path distance would be equal to the surface distance from CERN to Gran Sasso, again about 410 metres longer. This would have given the neutrino travel time difference to be an extra 410/c = 1370 ns, making the neutrinos travel significantly faster than the speed of light.

All of these experiments have shown that neutrino oscillation does occur, which means neutrinos have a non-zero mass. But we still don’t know what that mass is. It must be small enough that for all our existing experiments we can’t detect any any difference between the neutrino speed and the speed of light. More experiments are underway to try and pin down the nature of these elusive particles.

But importantly for our purposes, these neutrino beam experiments make no sense if the Earth is flat, and can only be interpreted correctly because we know the Earth is a globe.

References:

[1] “Long Baseline neutrino oscillation experiment, from KEK to Kamioka (K2K)”. KEK website. http://neutrino.kek.jp/intro/ (accessed 2019-10-01.)

[2] Louis, W. C. “Viewpoint: The antineutrino vanishes differently”. Physics, 4, p. 54, 2011. https://physics.aps.org/articles/v4/54

[3] MINOS collaboration, Adamson, P. et al. “Measurement of neutrino velocity with the MINOS detectors and NuMI neutrino beam”. Physical Review D, 76, p. 072005, 2007. https://doi.org/10.1103/PhysRevD.76.072005

[4] “Old accelerators image gallery”. CERN. https://home.cern/resources/image/accelerators/old-accelerators-images-gallery (accessed 2019-10-01).

[5] The OPERA collaboration, Adam, T., Agafonova, N. et al. “Measurement of the neutrino velocity with the OPERA detector in the CNGS beam”. Journal of High Energy Physics, 2012, p. 93, 2012. https://doi.org/10.1007/JHEP10(2012)093

10. The Sagnac effect

Imagine beams of light coming from an emitter and travelling around a circular path in both directions, until they arrive back at the source. Such an arrangement can be constructed by using an optic fibre in a circular loop, injecting light at both ends. The distance travelled by the clockwise beam is the same as the distance travelled by the anticlockwise beam, and the speed of light in both directions is the same, so the time taken for each beam to travel from the source back to the origin is the same. So far, so good.

A light loop

A loop with light travelling in both directions.

Now imagine the whole thing is rotating – let’s say clockwise. For reference we’ll use the numbers on a clock face and the finer divisions into 60 minutes. The optic fibre ring runs around the edge of the clock, with the light source and a detector at 12. Now imagine that the clock rotates fast enough that by the time the clockwise-going light reaches the original 12 position, the clock has rotated so that 12 is now located at the original 1 minute past 12 position. The light has to travel an extra 60th of the circle to reach its starting position (actually a tiny bit more than that because the clock is still rotating and will have gone a tiny bit further by the time the light beam catches up). But the light going anticlockwise reaches the source early, only needing to travel a tiny bit more than 59/60 of the circle. The travel times of the two beams of light around the circle are different.

A rotating light loop

Now the loop is rotating. By the time the light has travelled around the loop, the exit from the loop has moved a little bit clockwise. So the light travelling clockwise has to travel further to reach the exit, while the light travelling anticlockwise reaches the exit sooner.

This is a very simplified explanation, and figuring out the mathematics of exactly what happens involves using special relativity, since the speed of light is involved, but it can be shown that there is indeed a time difference between the travel times of beams of light heading in opposite directions around a rotating loop. The time difference is proportional to the speed of rotation and to the area of the loop (and to the cosine of the angle between the rotation axis and the perpendicular to the loop, for those who enjoy vector mathematics). This effect is known as the Sagnac effect, named after French physicist Georges Sagnac, who first demonstrated it in 1913.

Measuring the minuscule time difference between the propagation of the light beams is not difficult, due to the wave nature of light itself. The wavelength of visible light is just a few hundred nanometres, so even a time difference of the order of 10^-16 seconds can be observed because it moves the wave crests and troughs of the two beams relative to one another, causing visible interference patterns as they shift out of synchronisation. This makes the device an interferometer that is very sensitive to rotational speed.

The Sagnac effect can be seen not only in a circular loop of optic fibre, but also with any closed loop of light beams of any shape, such as can be constructed with a set of mirrors. This was how experimenters demonstrated the effect before the invention of optic fibres. Because the paths of the two beams of light are the same, just reversed, a Sagnac interferometer is completely insensitive to mechanical construction tolerances, and only sensitive to the physical rotation of the device.

Sagnac actually performed the experiment in an attempt to prove the existence of the luminiferous aether, a hypothetical medium permeating all space through which light waves propagate. He believed his results showed that such an aether existed, but Max von Laue and Albert Einstein showed that Sagnac’s effect could be explained by special relativity, without requiring any aether medium for light propagation.

The interesting thing about the Sagnac effect is that it measures absolute rotational speed, that is: rotation relative to an inertial reference frame, in the language of special relativity. In practice, this means rotation relative to the “fixed” position of distant stars. This is useful for inertial guidance systems, such as those found on satellites, modern airliners and military planes, and missiles. The Sagnac effect is used in ring laser gyroscopes and fibre optic gyroscopes to provide an accurate measure of rotational speed in these guidance systems. GPS satellites use these devices to ensure their signals are correctly calibrated for rotation – without them GPS would be less accurate.

Because the magnitude of the Sagnac effect depends on both the rotational speed and the area of the light loop, by making the area large you can make the interferometer incredibly sensitive to even very slow rotation. Rotations as slow as once per 24 hours. You can use these devices to measure the rotation of the Earth.

This was first done in 1925. Albert A. Michelson (of the famous Michelson-Morley experiment that disproved the existence of the luminiferous aether), Henry G. Gale, and Fred Pearson acquired the use of a tract of land in Clearing, Illinois (near Chicago’s Midway Airport), and built a huge Sagnac interferometer, a rectangle 610×340 metres in size [1][2].

Michelson’s Sagnac interferometer

Diagram of Michelson’s Sagnac interferometer in Clearing, Illinois. The Sagnac loop is defined by the mirrors ADEF. The smaller rectangle ABCD was used for calibration measurements. Light enters from the bottom towards the mirror A, which is half-silvered, allowing half the light through to D, and reflecting half in the other direction towards F. The beams complete circuits ADEF and AFED, returning to A, where the half-silvering reflects the beam from D and lets through the beam from F towards the detector situated outside the loop at the left. The light paths are inside a pipe system, which is evacuated using a pump to remove most of the air. (Figure reproduced from [2].)

With this enormous area, the shift in the light beams caused by the rotation speed of the Earth at the latitude of Chicago was around one fifth of a wavelength of the light used – easily observable. The Michelson-Gale-Pearson experiment’s measurements and calculations showed that the rotation speed they measured was consistent with the rotation of the Earth once every 23 hours and 56 minutes – a sidereal day (i.e. Earth’s rotation period relative to the stars; this is shorter than the average of 24 hours rotation relative to the sun, because the Earth also moves around the sun).

Now the interesting thing is that the Sagnac effect measures the linear rotation speed, not the angular rotation rate. The Earth rotates once per day – that angular rotation rate is constant for the entire planet, and can be modelled in a flat Earth model simply by assuming the Earth is a spinning disc, like a vinyl record or Blu-ray disc. But the linear rotation speed of points on the surface of the Earth varies.

In the typical flat Earth model with the North Pole at the centre of the disc, the rotation speed is zero at the North Pole, and increases linearly with distance from the Pole. As you cross the equatorial regions, the rotational speed just keeps increasing linearly, until it is maximal in regions near the “South Pole” (wherever that may be).

Rotation speed on a flat disc Earth

Rotation speeds at different places on a flat rotating disc Earth (top view of the disc).

On a spherical Earth, in contrast, the rotation speed is zero at the North Pole, and varies as the cosine of the latitude as you travel south, until it is a maximum at the equator, then drops again to zero at the South Pole.

Rotation speed on a flat disc Earth

Rotation speeds at different places on a spherical Earth.

Here is a table of rotation speeds for the two models:

Latitude	Speed (km/h) Flat model	Speed (km/h) Spherical model
90°N (North Pole)	0.0	0.0
60°N	875.3	837.2
41.77°N (Clearing, IL)	1407.2	1248.9
30°N	1750.5	1450.1
0° (Equator)	2625.8	1674.4
30°S	3501.1	1450.1
45.57°S (Christchurch)	3896.6	1213.3
60°S	4376.4	837.2
90°S (South Pole)	5251.6	0.0

In the Michelson-Gale-Pearson experiment, the calculated expected interferometer shift was 0.236±0.002 of a fringe (essentially a wavelength of the light used), and the observed shift was 0.230±0.005 of a fringe. The uncertainty ranges overlap, so the measurement is consistent with the spherical Earth model that they used to calculate the expected result.

If they had used the North-Pole-centred flat Earth model, then the expected shift would have been 1407.2/1248.9 larger, or 0.266±0.002 of a fringe. This is well outside the observed measurement uncertainty range. So we can conclude that Michelson’s original 1925 experiment showed that the rotation of the Earth is inconsistent with the flat Earth model.

Nowadays we have much more than that single data point. Sagnac interferometers are routinely used to measure the rotation speed of the Earth at various geographical locations. In just one published example, a device in Christchurch, New Zealand, at a latitude of 43°34′S, measured the rotation of the Earth equal to the expected value (for a spherical Earth) to within one part in a million [3]. Given that the expected flat Earth model speed is more than 3 times the spherical Earth speed at this latitude—and all of the other rotation speed measurements made all over the Earth consistent with a spherical Earth—we can well and truly say that any rotating disc flat Earth model is ruled out by the Sagnac effect.

References:
[1] Michelson, A. A. “The Effect of the Earth’s Rotation on the Velocity of Light, I.” The Astrophysical Journal, 61, 137-139, 1925. https://doi.org/10.1086%2F142878
[2] Michelson, A. A.; Gale, Henry G. “The Effect of the Earth’s Rotation on the Velocity of Light, II.” The Astrophysical Journal, 61, p. 140-145, 1925. https://doi.org/10.1086%2F142879
[3] Anderson, R.; Bilger, H. R.; Stedman, G. E. “ “Sagnac” effect: A century of Earth‐rotated interferometers”. American Journal of Physics, 62, p. 975-985, 1994. https://doi.org/10.1119/1.17656

Share this:

Share this: