Tag: particle physics

34. Earth’s internal heat

Opening disclaimer: I’m going to be talking about “heat” a lot in this one. Formally, “heat” is defined as a process of energy flow, and not as an amount of thermal energy in a body. However to people who aren’t experts in thermodynamics (i.e. nearly everyone), “heat” is commonly understood as an “amount of hotness” or “amount of thermal energy”. To avoid the linguistic awkwardness of using the five-syllable phrase “thermal energy” in every single instance, I’m just going to use this colloquial meaning of “heat”. Even some of the papers I cite use “heat” in this colloquial sense. I’ve already done it in the title, which to be technically correct should be the more awkward and less pithy “Earth’s internal thermal energy”.

The interior of the Earth is hot. Miners know first hand that as you go deeper into the Earth, the temperature increases. The deepest mine on Earth is the TauTona gold mine in South Africa, reaching 3.9 kilometres below sea level. At this depth, the rock temperature is 60°C, and considerable cooling technology is required to bring the air temperature down to a level where the miners can survive. The Kola Superdeep Borehole in Russia reached a depth of 12.2 km, where it found the temperature to be 180°C.

Lava, Hawaii

Lava—molten rock—emerging from the Earth in Hawaii. (Public domain image by the United States Geological Survey, from Wikimedia Commons.)

Deeper in the Earth, the temperature gets hot enough to melt rock. The results are visible in the lava that emerges from volcanic eruptions. How did the interior of the Earth get that hot? And exactly how hot is it down there?

For many years, geologists have been measuring the amount of thermal energy flowing out of the Earth, at thousands of measuring stations across the planet. A 2013 paper analyses some 38,374 heat flow measurements across the globe to produce a map of the mean heat flow out of the Earth, shown below[1]:

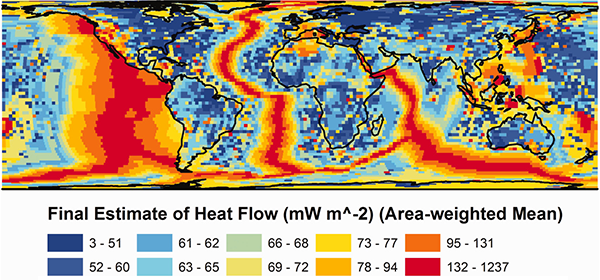
Mean heat flow out of the Earth

Mean heat flow out of the Earth in milliwatts per square metre, as a function of location. (Figure reproduced from [1].)

From the map, you can see that most of Earth’s heat emerges at the mid-ocean ridges, deep underwater. This makes sense, as this is where rising plumes of magma from deep within the mantle are acting to bring new rock material to the crust. The coolest areas are generally geologically stable regions in the middle of tectonic plates.

Hydrothermal vent

Subterranean material (and heat) emerging from a hydrothermal vent on Eifuku Seamount, Marianas Trench Marine National Monument. (Public domain image by the United States National Oceanic and Atmospheric Administration, from Wikimedia Commons.)

Although the heat flow out of the Earth’s surface is of the order of milliwatts per square metre, the surface has a lot of square metres. The overall heat flow out of the Earth comes to a total of around 47 terawatts[2]. In contrast, the sun emits close to 4×1014 terawatts of energy in total, and the solar energy falling on the Earth’s surface is 1360 watts per square metre, over 10,000 times as much as the heat energy leaking out of the Earth itself. So the sun dominates Earth’s heating and weather systems by roughly that factor.

So the Earth generates some 47 TW of thermal power. Where does this huge amount of energy come from? To answer that, we need to go all the way back to when the Earth was formed, some 4.5 billion years ago.

Our sun formed from the gaseous and dusty material distributed throughout the Galaxy. This material is not distributed evenly, and where there is a denser concentration, gravity acts to draw in more material. As the material is pulled in, any small motions are amplified into an overall rotation. The result is an accretion disc, with matter spiralling into a growing mass at the centre. When the central concentration accumulates enough mass, the pressure ignites nuclear reactions and a star is born. Some of the leftover material continues to orbit the new star and forms smaller accretions that eventually become planets or smaller bodies.

The process of accreting matter generates thermal energy. Gravitational potential energy reduces as matter pulls closer together, and the resulting collisions between matter particles convert it into thermal energy, heating up the accumulating mass. Our Earth was born hot. As the matter settled into a solid body, the shrinking further heated the core through the Kelvin-Helmholtz mechanism. The total heat energy from the initial formation of the Earth dissipates only very slowly into space, and that process is still going on today, 4.5 billion years later.

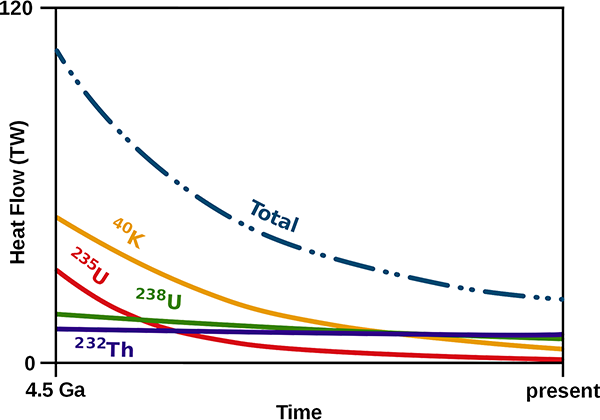
It’s not known precisely how much of this primordial heat is left in Earth or how much flows out, but various different studies suggest it is somewhere in the range of 12-30 TW, roughly a quarter to two-thirds of Earth’s total measured heat flux[3]. So that’s not the only source of the heat energy flowing out of the Earth.

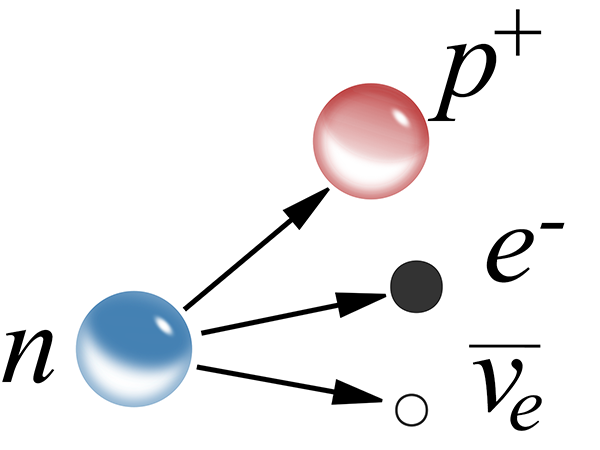
The other source of Earth’s internal heat is radioactive decay. Some of the matter in the primordial gas and dust cloud that formed the sun and planets was produced in the supernova explosions of previous generations of stars. These explosions produce atoms of radioactively unstable isotopes. Many of these decay relatively rapidly and are essentially gone by now. But some isotopes have very long half-lives, most importantly: potassium-40 (1.25 billion years), thorium-232 (14.05 billion years), uranium-235 (703.8 million years), and uranium-238 (4.47 billion years). These isotopes still exist in significant quantities inside the Earth, where they continue to decay, releasing energy.

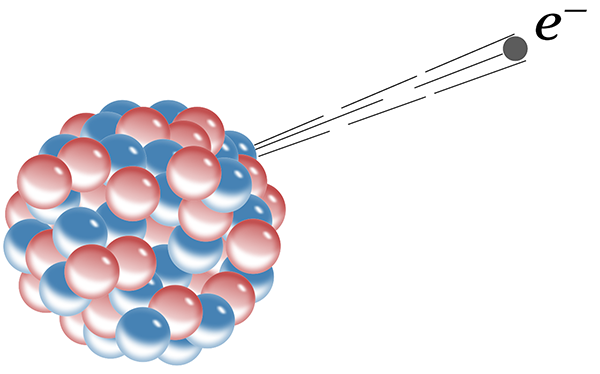
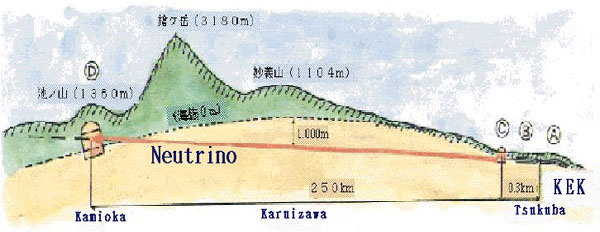
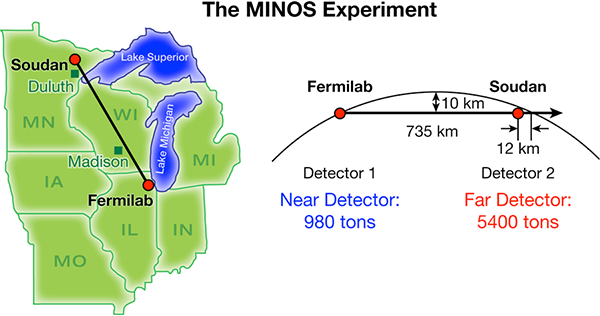
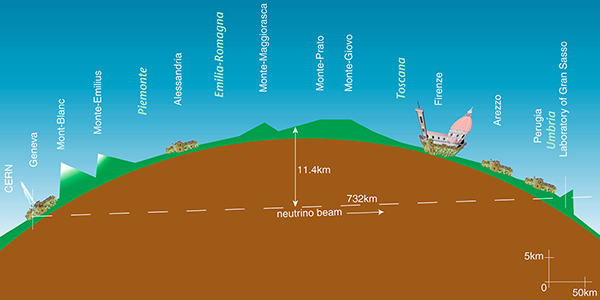
We have a way of probing how much radioactive energy is released inside the Earth. The decay reactions produce neutrinos (which we’ve met before), and because they travel unhindered through the Earth these can be detected by neutrino observatories. These geoneutrinos have energy ranges that distinguish them from cosmic neutrino sources, and of course always emerge from underground. The observed decay rates from geoneutrinos correspond to a total radiothermal energy production of 10-30 TW, of the same order as the primordial heat flux. (The neutrinos themselves also carry away part of the energy from the radioactive decays, roughly 5 TW, but this is an additional component not deposited as thermal energy inside the Earth.)

Mean heat flow out of the Earth

Approximate radiothermal energy generated within the Earth, plotted as a function of time, from the formation of the Earth 4.5 billion years ago, to the present. The four main isotopes are plotted separately, and the total is shown as the dashed line. (Public domain figure adapted from data in [4], from Wikimedia Commons.)

To within the uncertainties, the sum of the estimated primordial and measured radiothermal energy fluxes is equal to the total measured 47 TW flux. So that’s good.

Once you know how much heat is being generated inside the Earth, you can start to apply heat transfer equations, knowing the thermodynamic properties of rock and iron, how much conduction and convection can be expected, and cross-referencing it with our knowledge of the physical state of these materials under different temperature and pressure conditions. There’s also additional information about the internal structure of the Earth that we get from seismology, but that’s a story for a future article. Putting it all together, you end up with a linked series of equations which you can solve to determine the temperature profile of the Earth as a function of depth.

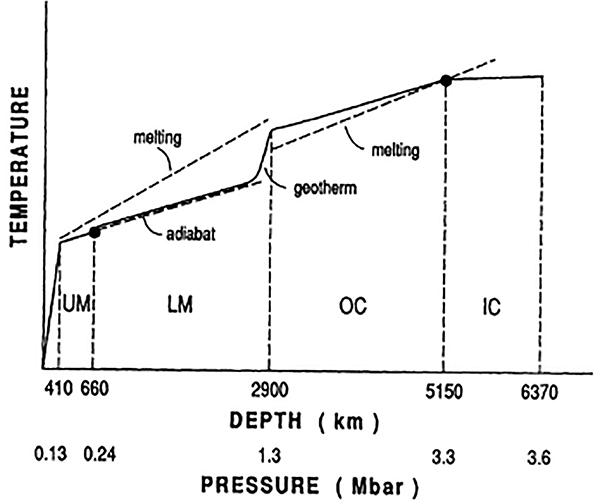
Mean heat flow out of the Earth

Temperature profile of the Earth’s interior, from the surface (left) to the centre of the core (right). Temperature units are not marked on the vertical axis, but the temperature of the surface (bottom left corner) is approximately 300 K, and the inner core (IC, right) is around 7000 K. UM is upper mantle, LM lower mantle, OC outer core. The calculated temperature profile is the solid line. The two solid dots are fixed points constrained by known phase transitions of rock and iron – the slopes of the curves between them are governed by the thermodynamic equations. The dashed lines are various components of the constraining equations. (Figure reproduced from [5].)

The results are all self-consistent, with observations such as the temperature of the rock in deep mine shafts and the rate of detection of geoneutrinos, with structural constraints provided by seismology, and with the temperature constraints and known modes of heat flow from the core to the surface of the Earth.

That is, they’re all consistent assuming the Earth is a spherical body of rock and iron. If the Earth were flat, the thermal transport equations would need to be changed to reflect the different geometry. As a first approximation, assume the flat Earth is relatively thin (i.e. a cylinder with the radius larger than the height). We still measure the same amount of heat flux emerging from the Earth’s surface, so the same amount of heat has to be either (a) generated inside it, or (b) being input from some external energy source underneath the flat Earth. However geoneutrino energy ranges indicate that they come from radioactive decay of Earthly minerals, so it makes sense to conclude that radiothermal heating is significant.

If radioactive decay is producing heat within the bulk of the flat Earth, then half of the produced neutrinos will emerge from the underside, and thus be undetectable. So the total heat production should be double that deduced from neutrino observations, or somewhere in the range 20-60 TW. To produce twice the energy, you need twice the mass of the Earth. If the flat Earth is a disc with radius 20,000 km (the distance from the North Pole to the South Pole), then to have the same volume as the spherical Earth it would need to be 859 km thick. But we need twice as much mass to produce the observed thermal energy flux, so it should be approximately 1720 km thick. Some fraction of the geoneutrinos will escape from the sides of the cylinder of this thickness, which means we need to add more rock to produce a bit more energy to compensate, so the final result will be a bit thicker.

There’s no obvious reason to suppose that a flat Earth can’t be a bit over 1700 km thick, as opposed to any other thickness. With over twice as much mass as our spherical Earth, the surface gravity of this thermodynamically correct flat Earth would be over 2 Gs (i.e. twice the gravity we experience), which is obviously wrong, but then many flat Earth models deny Newton’s law of gravity anyway (because it causes so many problems for the model).

But just as in the spherical Earth model the observed geoneutrino flux only accounts for roughly half the observed surface heat flux. The other half could potentially come from primordial heat left over from the flat Earth’s formation – although as we’ve already seen, what we know about planetary formation precludes the formation of a flat Earth in the first place. The other option is (b) that the missing half of the energy is coming from some source underneath the flat Earth, heating it like a hotplate. What this source of extra energy is is mysterious. No flat Earth model that I’ve seen addresses this problem, let alone proposes a solution.

What’s more, if such a source of energy under the flat Earth existed, then it would most likely also radiate into space around the edges of the flat Earth, and have observable effects on the objects in the sky above us. What we’re left with, if we trust the sciences of radioactive decay and thermal energy transfer, is a strong constraint on the thickness of the flat Earth, plus a mysterious unspecified energy source underneath – neither of which are mentioned in standard flat Earth models.

References:

[1] Davies, J. H. “Global map of solid Earth surface heat flow”. Geochemistry, Geophysics, Geosystems, 14(10), p.4608-4622, 2013. https://doi.org/10.1002/ggge.20271

[2] Davies, J.H., Davies, D.R. “Earth’s surface heat flux”. Solid Earth, 1(1), p.5-24, 2010. https://doi.org/10.5194/se-1-5-2010

[3] Dye, S.T. “Geoneutrinos and the radioactive power of the Earth”. Reviews of Geophysics, 50(3), 2012. https://doi.org/10.1029/2012RG000400

[4] Arevalo Jr, R., McDonough, W.F., Luong, M. “The K/U ratio of the silicate Earth: Insights into mantle composition, structure and thermal evolution”. Earth and Planetary Science Letters, 278(3-4), p.361-369, 2009. https://doi.org/10.1016/j.epsl.2008.12.023

[5] Boehler, R. “Melting temperature of the Earth’s mantle and core: Earth’s thermal structure”. Annual Review of Earth and Planetary Sciences, 24(1), p.15-40, 1996. https://doi.org/10.1146/annurev.earth.24.1.15

29. Neutrino beams

We’ve met neutrinos before, when talking about supernova 1987A.

Historically, the early quantum physicist Wolfgang Pauli first proposed the existence of the neutrino in 1930, to explain a problem with then-current understanding of radioactive beta decay. In beta decay, an atomic nucleus emits an electron, which has a negative electric charge, and the resulting nucleus increases in positive charge, transmuting into the element with the next highest atomic number. The law of conservation of energy applied to this nuclear reaction implied that the electron should be emitted from any given isotope with a specific energy, balancing the change in mass as given by Einstein’s famous E = mc2 (energy equals mass times the speed of light squared). Alpha particles emitted during alpha decay, and gamma rays emitted during gamma decay appear at fixed energies.

beta decay, early conception

Illustration of beta decay. The nucleus at left emits an electron. (Public domain image from Wikimedia Commons.)

However, this was not what was observed for beta decay electrons. The ejected electrons had a maximum energy as predicted, but also appeared with a spread of lower energies. Pauli suggested that another particle was involved in the beta decay reaction, which carried off some of the energy. In a three-body reaction, the energy could be split between the electron and the new particle in a continuous fashion, thus explaining the spread of electron energies. Pauli suggested the new particle must be very light, so as to evade detection up to that time. He called it a “neutron”, a neutral particle following the word-ending convention of electron and proton.

However, in the same year German physicists Walther Bothe and Herbert Becker produced some strange radiation by bombarding light elements with alpha particles from radioactive polonium. This radiation had properties unlike other forms known at the time, and several experimenters tried to understand it. In 1932, James Chadwick performed experiments that demonstrated the radiation was made of neutral particles of about the same mass as a proton. The name “neutron” had been floating around nuclear physics for some time (Pauli wasn’t the first to use it; “neutron” appears in the literature as a name for proposed hypothetical neutral particles as early as 1899), but Chadwick was the first experimenter to demonstrate the existence of a neutral particle, so the name got attached to his discovery. Italian physicist Enrico Fermi responded by referring to Pauli’s proposed very light neutral particle as a “neutrino”, or “little neutron” in Italian coinage.

beta decay

Beta decay. A neutron decays to produce a proton, an electron, and an electron anti-neutrino. The neutrino produced has to be an antiparticle to maintain matter/antimatter balance, though it is often referred to simply as a “neutrino” rather than an anti-neutrino. (Public domain image from Wikimedia Commons.)

Detection of the neutrino had to wait until 1956, when a sensitive enough experiment could be performed, by American physicists Clyde Cowan and Frederick Reines, for which Reines received the 1995 Nobel Prize in Physics (Cowan had unfortunately died in 1974). In 1962, Leon Lederman, Melvin Schwartz, and Jack Steinberger of Fermilab discovered that muons—particles similar to electrons but with more mass—had their own associated neutrinos, distinct from electron neutrinos. They received the Nobel Prize for this discovery in 1988 (only a 26 year wait, unlike Reines’ 39 year wait). Finally, Martin Perl discovered a third, even more massive electron-like particle, named the tau lepton, in 1975, for which he shared that 1995 Prize with Reines. The tau lepton, like the electron and muon, has its own distinct associated neutrino.

Meanwhile, other researchers had been building neutrino detectors to observe neutrinos emitted by the sun’s nuclear reactions. Neutrinos interact only extremely weakly with matter, so although approximately 7×1014 solar neutrinos hit every square metre of Earth every second, almost none of them affect anything, and in fact almost all of them pass straight through the Earth and continue into space without stopping. To detect neutrinos you need a large volume of transparent material; water is usually used. Occasionally one neutrino of the trillions that pass through every second will interact, causing a single-atom nuclear reaction that produces a brief flash of light, which can then be seen by light detectors positioned around the periphery of the transparent material.

Daya Bay neutrino detector

Interior of the Daya Bay Reactor neutrino detector, China. The glassy bubbles house photodetectors to detect the flashes of light produced by neutrino interactions in the liquid filled interior (not filled in this photo). (Public domain image by U.S. Department of Energy, from Wikimedia Commons.)

When various solar neutrino detectors were turned on, there was a problem. They detected only about one third to one half of the number of neutrinos expected from models of how the sun works. The physics was thought to be well understood, so there was great trouble trying to reconcile the observations with theory. One of the least “break everything else we know about nuclear physics” proposals was that perhaps neutrinos could spontaneously and randomly change flavour, converting between electron, muon, and tau neutrinos. The neutrino detectors could only detect electron neutrinos, so if the neutrinos generated by the sun could change flavour (a process known as neutrino oscillation) during the time it took them to arrive at Earth, the result would be a roughly equal mix of the three flavours, so the detectors would only see about a third of them.

Another unanswered question about neutrinos was whether they had mass or not. Neutrinos have only ever been detected travelling at speeds so close to the speed of light that we weren’t sure if they were travelling at the speed of light (in which case they must be massless, like photons) or just a tiny fraction below it (in which case they must have a non-zero mass). Even the neutrinos detected from supernova 1987A, 168,000 light years away, arrived before the initial light pulse from the explosion (because the neutrinos passed immediately out of the star’s core, while the light had to contend with thousands of kilometres of opaque gas before being released), so we weren’t sure if they were travelling at the speed of light or just very close to it. Interestingly, the mass of neutrinos is tied to whether they can change flavour: if neutrinos are massless, then they can’t change flavour, whereas if they have mass, then they must be able to change flavour.

To test these properties, particle physicists began performing experiments to see if neutrinos could change flavour. To do this, you need to produce some neutrinos and then measure them a bit later to see if you can detect any that have changed flavour. But because neutrinos move at very close to the speed of light, you can’t detect them at the same place you create them; you need to have your detector a long way away. Preferably hundreds of kilometres or more.

The first such experiment was the KEK to Kamioka, or K2K experiment, running from 1999-2004. This involved the Japanese KEK laboratory in Tsukuba generating a beam of muon neutrinos and aiming the beam at the Super-Kamiokande neutrino detector at Kamioka, a distance of 250 kilometres away.

K2K map

Map of central Japan, showing the locations of KEK and Super-Kamiokande. (Figure reproduced from [1].)

The map is from the official website of KEK. Notice that Super-Kamiokande is on the other side of a mountain range from KEK. But this doesn’t matter, because neutrinos travel straight through solid matter! Interestingly, here’s another view of the neutrino path from the KEK website:

K2K cross section

Cross sectional view of neutrino beam path from KEK to Super-Kamiokande. (Figure reproduced from [1].)

You can see that the neutrino beam passes underneath the mountains from KEK to the underground location of the Super-Kamiokande detector, in a mine 1000 metres below Mount Ikeno (altitude 1360 m). KEK at Tsukuba is at an altitude of 35 m. Now because of the curvature of the Earth, the neutrino beam passes in a straight line 1000 m below sea level at its middle point. With the radius of the Earth 6367 km, Pythagoras’ theorem tells us that the centre of the beam path is 6365.8 km from the centre of the Earth, so 1200 m below the mean altitude of KEK and Super-Kamiokande – the maths works out. Importantly, the neutrino beam cannot be fired horizontally, it has to be aimed at an angle of about 0.5° into the ground for it to emerge correctly at Super-Kamiokande.

The K2K experiment succeeded in detecting a loss of muon neutrinos, establishing that some of them were oscillating into other neutrino flavours.

A follow up experiment, MINOS, began in 2005, this time using a neutrino beam generated at Fermilab in Illinois, firing at a detector located in the Soudan Mine in Minnesota, some 735 km away.

MINOS map and cross section

Map and sectional view of the MINOS experiment. (Figure reproduced from [2].)

In this case, the straight line neutrino path passes 10 km below the surface of the Earth, requiring the beam to be aimed downwards at an angle of 1.6° in order to successfully reach the detector. Another thing that MINOS did was to measure the time of flight of the neutrino beam between Fermilab and Soudan. When they sent a pulsed beam and measured the time taken for the pulse to arrive at Soudan, then divided it by the distance, they concluded that the speed of the neutrinos was between 0.999976 and 1.000126 times the speed of light, which is consistent with them not violating special relativity by exceeding the speed of light[3].

If you measure the distance from Fermilab to Soudan along the curvature of the Earth, as you would do for normal means of travel (or if the Earth were flat), you get a distance about 410 metres (or 0.06%) longer than the straight line distance through the Earth that the neutrinos took. If the scientists had used that distance, then their neutrino speed measurements would have given values 0.06% higher: 1.00053 to 1.00068 times the speed of light. In other words, to get a result that doesn’t violate known laws of physics, you have to take account of the fact that the Earth is spherical, and not flat.

This result has been reproduced with reduced uncertainty bounds by the CERN Neutrinos to Gran Sasso (CNGS) experiment in Europe, which fires a neutrino beam from CERN in Switzerland to the OPERA detector at the Gran Sasso National Laboratory in Italy.

CNGS cross section

Sectional view of the CNGS experiment neutrino beam path. (Image is Copyright CERN, used under CERN Terms of Use, from [4].)

The difference between the neutrino travel times and the speed of light over the 732 km beam path was measured to be -1.9±3.7 nanoseconds, consistent with zero difference[5]. In this case, if a flat Earth model had been used, the beam path distance would be equal to the surface distance from CERN to Gran Sasso, again about 410 metres longer. This would have given the neutrino travel time difference to be an extra 410/c = 1370 ns, making the neutrinos travel significantly faster than the speed of light.

All of these experiments have shown that neutrino oscillation does occur, which means neutrinos have a non-zero mass. But we still don’t know what that mass is. It must be small enough that for all our existing experiments we can’t detect any any difference between the neutrino speed and the speed of light. More experiments are underway to try and pin down the nature of these elusive particles.

But importantly for our purposes, these neutrino beam experiments make no sense if the Earth is flat, and can only be interpreted correctly because we know the Earth is a globe.

References:

[1] “Long Baseline neutrino oscillation experiment, from KEK to Kamioka (K2K)”. KEK website. http://neutrino.kek.jp/intro/ (accessed 2019-10-01.)

[2] Louis, W. C. “Viewpoint: The antineutrino vanishes differently”. Physics, 4, p. 54, 2011. https://physics.aps.org/articles/v4/54

[3] MINOS collaboration, Adamson, P. et al. “Measurement of neutrino velocity with the MINOS detectors and NuMI neutrino beam”. Physical Review D, 76, p. 072005, 2007. https://doi.org/10.1103/PhysRevD.76.072005

[4] “Old accelerators image gallery”. CERN. https://home.cern/resources/image/accelerators/old-accelerators-images-gallery (accessed 2019-10-01).

[5] The OPERA collaboration, Adam, T., Agafonova, N. et al. “Measurement of the neutrino velocity with the OPERA detector in the CNGS beam”. Journal of High Energy Physics, 2012, p. 93, 2012. https://doi.org/10.1007/JHEP10(2012)093

7. Supernova 1987A

[audio version of this article]

Stars produce energy from nuclear fusion reactions in their cores, where the light elements making up the bulk of the star are compressed and heated by gravity until they fuse into heavier elements. There is a limit to this, however, because once iron is produced in the core no more energy can be extracted from it. Fusing iron requires an input of energy. As iron accumulates, the layers near the core collapse inwards, because not enough energy is being produced to hold them up. At a certain point, the collapse speeds up suddenly and catastrophically, the whole core of the star collapsing in a few seconds. This releases an enormous amount of gravitational energy, fusing heavier elements and initiating nuclear reactions in the outer parts of the star, which blow off in a vast explosion. The star has turned into a supernova, one of the most energetic phenomena in the universe. A supernova can, briefly, shine brighter than the entire galaxy of 100 billion (1011) stars containing it.

Historically, supernovae were detected visually, when a “new star” suddenly appeared in the night sky, shining brightly for a few weeks before fading away from sight. We have reliable records of visible supernovae appearing in the years 1006, 1054, 1181, 1572, and 1604, as well as unconfirmed but probable events occurring in 185 and 393. These supernovae all occurred within our own Milky Way Galaxy, so were close enough to be visible to the naked eye. Since 1604, there have been no supernovae detected in our Galaxy – which is a bit of a shame because the telescope was invented around 1608, just too late to observe the most recent one.

Astronomers have used telescopes to observe supernovae in other galaxies since the late 19th century. Almost none of these are visible to the naked eye. But in 1987 a supernova occurred in the Large Magellanic Cloud, a dwarf galaxy satellite of our own, making it the nearest supernova ever observed in the telescopic era. It reached magnitude 3, making it as bright as a middling star in our sky. It was first seen by independent observers in Chile and New Zealand on 24 February 1987.

The Large Magellanic Cloud is visible from the southern hemisphere of Earth, and in the north up to a latitude around 21°N. It is never visible from any point further north. And so supernova 1987A (the first supernova detected in 1987) was never visible from any point further north than 21°N.

Supernova 1987A

Supernova 1987A and the Large Magellanic Cloud. SN 1987A is the bright star just right of the centre of the image. (Photo: Creative Commons Attribution 4.0 International by the European Southern Observatory.)

When a supernova explosion occurs, the collapsing star emits vast quantities of matter and radiation into the surrounding space. Visible light is just one part of the radiation. SN 1987A also emitted gamma rays, x-rays, and ultraviolet light, the latter two of which were detected by space-based telescopes. And it also blasted particles into interstellar space: heavy element nuclei, neutrons, electrons, and other subatomic particles. One of the types of particles produced was neutrinos. Neutrinos have such a small mass that so far we’ve been unable to perform any experiment that can distinguish their mass from zero. And this means that they move at close to the speed of light – so close that we’ve never made any observation that shows them to move any slower.

At the moment of collapse, SN 1987A emitted a huge burst of neutrinos. These travelled through intergalactic space and some of the neutrinos made it to Earth, where some of them were detected. This neutrino burst was detected almost simultaneously at three different neutrino observatories in different parts of the world:

While a total of 24 neutrinos might not sound like a lot, this is significantly higher than the background detection rate of neutrinos from other sources such as our sun and general cosmic rays from random directions in space. And all 24 of these neutrinos were detected within a single 13-second time window – if corrected for the differences in light travel time from SN 1987A to each observatory caused by their locations on the spherical Earth.

You might notice that all three of the detectors listed are in the northern hemisphere. In fact, the southernmost of them is Kamioka, at 36° 20′ 24″ N. This means that the Large Magellanic Cloud, and SN 1987A in particular, are not visible in the sky at any of these detector locations. This fact by itself provides fairly convincing evidence to most people that the Earth cannot be flat, but Flat Earth enthusiasts propose various solutions for the limited visibility of celestial objects from different parts of the Earth. In Flat Earth theory, all visible stars and galaxies are above the plane of the Earth, and obscured from some parts by distance or intervening objects. This obviously requires SN 1987A to be above the plane of the Flat Earth.

In fact, at this point it might seem that the spherical Earth has a problem: If SN 1987A is not visible from the locations of the neutrino detectors, then how did they detect neutrinos from it? The answer is that neutrinos are extremely elusive particles – they barely interact with matter at all. Neutrinos are known to pass right through the Earth with ease. So although the spherical Earth blocked the light from SN 1987A from reaching the neutrino observatories, it did not stop the neutrinos. The neutrinos passed through the Earth to reach the observatories.

Astronomers estimate SN 1987A released around 1058 neutrinos. The blast was 168,000 light years away, so at the distance of Earth, the number of neutrinos passing through the Earth would be approximately 3×1020 neutrinos per square metre. The Kamiokande-II detector is a cylinder of water 16 metres high and 15.6 metres in diameter, so nearly 1023 SN 1987A neutrinos would have passed through it, leading to just 11 detections. This matches the expected detection rate for neutrinos very well.

Additionally, the Kamioka and Irvine-Michigan-Brookhaven detectors are directional – they can determine the direction from which observed neutrinos arrive. They arrived coming up from underground, not down from the sky. The observed directions at both detectors correspond to the position of the Large Magellanic Cloud and SN1987A on the far side of the spherical Earth [1][2].

Kamiokande-II results

Distribution of SN 1987A neutrino detections at Kamiokande-II in energy of produced electrons and angle relative to the direction of the Large Magellanic Cloud (LMC). Detected electrons are produced by two different processes, the first is rapid and highly aligned with neutrino direction, while the second is a slower secondary particle generation process and randomises direction uniformly. Neutrinos 1 and 2 (the earliest in the burst) are aligned directly with the LMC, and the remainder are distributed uniformly. This is statistically consistent with the burst having originated from the LMC. Figure reproduced from [1].

In a flat Earth model, SN 1987A would have to be simultaneously above the plane of the Earth (to be visible from the southern hemisphere) and below it (for the neutrino burst to be visible coming up from under the plane of the Earth). This is self-contradictory. However the observations of SN 1987A are all consistent with the Earth being a globe.

References:

[1] Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; Suda, T.; Takahashi, K.; Tanimori, T.; Miyano, K.; Yamada, M.; Beier, E. W.; Feldscher, L. R.; Kim, S. B.; Mann, A. K.; Newcomer, F. M.; Van, R.; Zhang, W.; Cortez, B. G. “Observation of a neutrino burst from the supernova SN1987A”. Physical Review Letters, 58, p. 1490-1493, 1987. https://doi.org/10.1103/PhysRevLett.58.1490

[2] Bratton, C. B.; Casper, D.; Ciocio, A.; Claus, R.; Crouch, M.; Dye, S. T.; Errede, S.; Gajewski, W.; Goldhaber, M.; Haines, T. J.; Jones, T. W.; Kielczewska, D.; Kropp, W. R.; Learned, J. G.; Losecco, J. M.; Matthews, J.; Miller, R.; Mudan, M.; Price, L. R.; Reines, F.; Schultz, J.; Seidel, S.; Sinclair, D.; Sobel, H. W.; Stone, J. L.; Sulak, L.; Svoboda, R.; Thornton, G.; van der Velde, J. C. “Angular distribution of events from SN1987A”. Physical Review D, 37, p. 3361-3363, 1988. https://doi.org/10.1103/PhysRevD.37.3361