Tag: navigation

35. The Eötvös effect

In the opening years of the twentieth century, scientists in the field of geodesy (measuring the shape and gravitational field of the Earth) were interested in making measurements of the strength of gravity all over the Earth’s surface. To do this, they trekked to remote regions of the world with sensitive gravimeters, to take the readings. On land this was straightforward enough, but they also wanted measurements taken at sea.

Around 1900, teams from the Institute of Geodesy in Potsdam took voyages into the Atlantic, Indian, and Pacific Oceans on ships, and made measurements using their gravimeters. The collected data were brought back to Potsdam for analysis. There, the readings fell under the scrutinising eyes of the Hungarian physicist Loránd Eötvös, who specialised in studying the variation of Earth’s gravitational field with position on the surface. He noticed an odd thing about the readings.

Loránd Eötvös

Loránd Eötvös. (Public domain image from Wikimedia Commons.)

Because of the impracticality of stopping the ship every time they wanted to take a reading, the scientists measured the Earth’s gravity while the ships were moving. There was no reason to suppose this would make any difference. But Eötvös found a systematic effect. Gravity measurements taken while the ship was moving eastward were lower than readings taken while the ship was moving westward.

Eötvös realised that this effect was being caused by the rotation of the Earth. The Earth’s equatorial circumference is 40,075 km, and it rotates eastward once every sidereal day (23 hours, 56 minutes). So the ground at the equator is rotating at a linear speed of 465 metres per second. To move in a circular path rather than a straight line (as dictated by Newton’s First Law of Motion), gravity supplies a centripetal force to any object on the Earth’s surface. The necessary force is equal to the object’s mass times the velocity squared, divided by the radius of the circular path (6378 km). This comes to m×4652/6378000 = 0.0339m. So per kilogram of mass, a force of 0.0339 newtons is needed to enforce the circular path, an amount easily supplied by the Earth’s gravity. (This is why objects don’t get flung off the Earth by its rotation, a complaint of some spherical Earth sceptics.)

What this means is that the effective acceleration due to gravity measured for an object sitting on the equator is reduced by 0.0339 m/s2 (the same units as 0.0339 N/kg) compared to if the Earth were not rotating. But if you’re on a ship travelling east at, say, 10 m/s, the centripetal force required to keep you on the Earth’s surface is greater, equal to 4752/6378000 = 0.0354 N/kg. This reduces the apparent measured gravity by a larger amount, making the measured value of gravity smaller. And if you’re on a ship travelling west at 10 m/s, the centripetal force is 4552/6378000 = 0.0324 N/kg, reducing the apparent gravity by a smaller amount and making the measured value of gravity greater. The difference in apparent gravity between the ships travelling east and west is 0.003 m/s2, which is about 0.03% of the acceleration due to gravity. For a person of mass 70 kg, this is a difference in apparent weight of about 20 grams (strictly speaking, a difference in weight of 0.2 newtons, which is 20 grams multiplied by acceleration due to gravity).

Eötvös set out these theoretical calculations, and then organised an expedition to measure and test his results. In 1908, the experiment was carried out on board a ship in the Black Sea, with two separate ships travelling east and west past one another so the measurements could be made at the same time. The results matched Eötvös’s predictions, thus confirming the effect.

In general (if you’re not at the equator), your linear speed caused by the rotation of the Earth is equal to 465 m/s times the cosine of your latitude, while the radius of your circular motion is also equal to 6378 km times the cosine of your latitude. The centripetal force formula uses the square of the velocity divided by the radius, so this results in a cosine(latitude) term in the final result. That is, the size of the Eötvös effect also varies as the cosine of the latitude. If you measure it at 60° latitude, either north or south, the difference in gravity between east and west travelling ships is half that measured at the equator.

The Eötvös effect is well known in the field of gravimetry, and is routinely corrected for when taking measurements of the Earth’s gravitational strength from moving ships[1], aircraft[2], or submarines[3]. The reference on submarines refers to a gravitational measurement module for use on military submarines to enhance their navigation capability as undersea instruments of warfare. This module includes an Eötvös effect correction for when the sub is moving east or west. You can bet your bottom dollar that no military force in the world would make such a correction to their navigation instruments if it weren’t necessary.

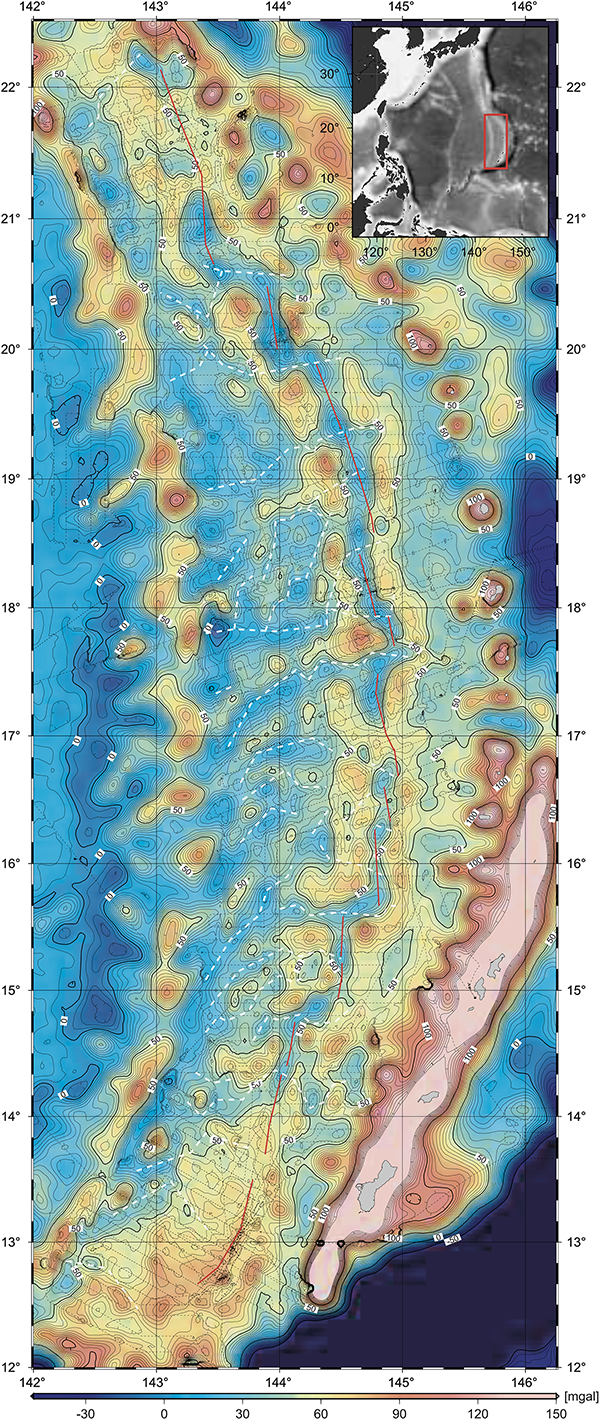
One paper I found reports measurements made of the detailed structure of gravitational anomalies over the Mariana Trough in the Pacific Ocean south of Japan. It states:

Shipboard free-air gravity anomalies were calculated by subtracting the normal gravity field data from observed gravity field data, with a correction applied for the Eötvös effect using Differential Global Positioning System (DGPS) data.[4]

The results look pretty cool:

Mariana Trough gravity anomalies map

Map of gravitational anomalies in the Mariana Trough region of the Pacific Ocean, as obtained by shipboard measurement, corrected for the Eötvös effect. (Figure reproduced from [4].)

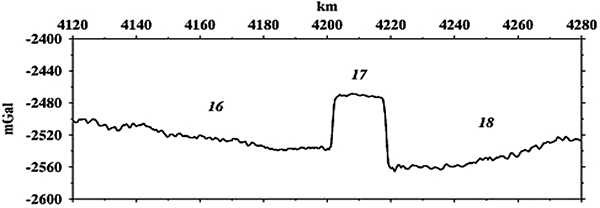
Another paper shows the Eötvös effect more directly:

Gravity measurements from moving ship

Graph showing measurements of Earth’s gravitational field strength versus distance travelled by a ship in the South Indian Ocean. In the leftmost section (16), the ship is moving slowly westward. In the central section (17) the ship is moving at a faster speed westward, showing the increase in measured gravity. In the right section (18) the ship is moving eastward at slow speed, and the gravity readings are lower than the readings taken in similar positions while moving westward. (Figure reproduced from [5].)

If the Earth were flat, on the other hand, there would be no Eötvös effect at all. If the flat Earth is not rotating (as most models posit, with the sun moving above it in a circular path), obviously there is no centripetal acceleration happening at all. Even if you adopt a model where the flat Earth rotates about the North Pole, the centripetal acceleration at every point on the surface is parallel to the surface, towards the pole, not directed downwards. So an Eötvös-like effect would actually cause a slight deflection in the angle of gravity, but almost zero change in the magnitude of the gravity.

The Eötvös effect shows that not only is the Earth rotating, but that it is rotating about a central point that is underneath the ground, not somewhere on the surface. If you stand on the equator and face east, the surface of the Earth is rotating in the direction you are facing and downwards, not to the left or right. Furthermore, the cosine term shows that at equal latitudes both north and south, the rotation is at the same angle relative to the surface, which can only be the case if the Earth is symmetrical about the equator: i.e. spherical.

References:

[1] Rousset, D., Bonneville, A., Lenat, J.F. “Detailed gravity study of the offshore structure of Piton de la Fournaise volcano, Réunion Island”. Bulletin of Volcanology, 49(6), p. 713-722, 1987. https://doi.org/10.1007/BF01079822

[2] Thompson, L.G., LaCoste, L.J. “Aerial gravity measurements”. Journal of Geophysical Research, 65(1), p. 305-322, 1960. https://doi.org/10.1029/JZ065i001p00305

[3] Moryl, J., Rice, H., Shinners, S. “The universal gravity module for enhanced submarine navigation”. In IEEE 1998 Position Location and Navigation Symposium, p. 324-331, April 1996. https://doi.org/10.1109/PLANS.1998.670124

[4] Kitada, K., Seama, N., Yamazaki, T., Nogi, Y., Suyehiro, K., “Distinct regional differences in crustal thickness along the axis of the Mariana Trough, inferred from gravity anomalies”. Geochemistry, Geophysics, Geosystems, 7(4), 2006. https://doi.org/10.1029/2005GC001119

[5] Persson, A. “The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885”. History of Meteorology, 2, p.1-24, 2005. https://www.semanticscholar.org/paper/The-Coriolis-Effect%3A-Four-centuries-of-conflict-and-Persson/c9e72567af65e44384fba048bbf491d3ac3a30ff

23. Straight line travel

Travel in a straight line across the surface of the Earth in any direction. After approximately 40,000 kilometres, you will find you are back where you started, having arrived from the opposite direction. While this sort of thing might be common in the wrap-around maps of some 1980s era video games, the simplest explanation for this in the real world is that the Earth is a globe, with a circumference about 40,000 km.

It’s difficult to see how this sort of thing could be possible on a flat Earth, unless the flat Earth’s surface were subject to some rather extreme directional and distance warping—that exactly mimics the behaviour of the surface of a sphere in Euclidean space. While this is not a priori impossible, it would certainly be an unlikely coincidence. Occam’s razor suggests that if it looks like a duck, quacks like a duck, and perfectly mimics the Euclidean geometry of a duck, it’s a duck.

This could be a very short and sweet entry if I left things there, but there are a few dangling questions.

Firstly there’s the question of exactly what we mean by a “straight line”. The Earth’s surface is curved, so any line we draw on it is necessarily curved in the third dimension, although this curvature is slight at scales we can easily perceive. The common understanding of a “straight line” on the Earth’s surface is the line giving the shortest distance joining two points as measured along the surface. This is what we mean when we talk about “straight lines” on Earth in casual speech, and it also matches how we’re using the term here.

In three dimensions, such “straight lines” are what we call great circles. A great circle is a circle on the surface of a sphere that has the same diameter as the sphere itself. On an idealised perfectly spherical Earth, the equator is a great circle, as are all of the meridians (i.e. lines of longitude). Lines of latitude other than the equator are not great circles: if you start north of the equator and travel due west, maintaining a westerly heading, then you are actually curving to the right. It’s easiest to see this by imagining a starting point very close to the North Pole. If you travel due west you will travel in a small clockwise circle around the pole.

Great circles

Great circles on a sphere. The horizontal circle is an equator, the vertical circle is a meridian, the red circle is an arbitrary great circle at some other angle.

Secondly, how can we know that we are travelling in such a straight line? The MythBusters once tested the myth that “It is impossible for a blindfolded person to travel in a straight line” and found that with restricted vision they were unable to either walk, swim, or drive in a straight line over even a very short distance[1]. We don’t need to keep our eyes closed though!

When travelling through unknown terrain, you can navigate by using the positions of the sun and stars as a reference frame, giving you a way of determining compass directions. Converting this into a great circle path however requires geometric calculations that depend on the spherical geometry of the Earth, so this approach is a somewhat circular argument if our aim is to demonstrate that the Earth is spherical.

A more direct method to ensure straight line travel is to line up two landmarks in the direction you are travelling, then when you reach the first one, line up another beyond the next one and repeat the process. This procedure can keep your course reasonably straight, but relies on visible and static landmarks, which may not be conveniently present. And this method is useless at sea.

Modern navigation now uses GPS to establish a position accurate to within a few metres. While this could be (and is routinely) used to plot a straight line course, again this relies on geometrical calculations that assume the Earth is spherical. (It works, of course, because the Earth is spherical, but render this particular line of argument against a flat Earth circular.)

Before GPS became commonplace, there was a different sort of navigation system in common use, and it is still used today as a backup for times when GPS is unavailable for any reason. These older systems are called inertial navigation systems (INS). They use components that provide an inertial frame of reference—that is, a reference frame that is not rotating or accelerating—independent of any motion of the Earth. These systems can be used for dead reckoning, which is navigating by plotting your direction and speed from your starting location to determine where you are at any time. They can be used to ensure that you follow a straight line path across the Earth, with reference to the inertial frame.

Inertial navigation systems can be built using several different physical principles, including mechanical gyroscopes, accelerometers, or laser ring gyroscopes utilising the Sagnac effect (previously discussed in these proofs). These systems drift in accuracy over time due to mechanical and environmental effects. Modern inertial navigation systems are accurate to 0.6 nautical miles per hour[2], or just over 1 km per hour. A plane flying at Mach 1 can fly a great circle route in just over 32 hours, so if relying only on INS it should arrive within 32 km of its starting point, which is close enough that a pilot can figure out that it’s back where it started. So in principle we can do this experiment with current technology.

A great circle on our spherical Earth is straightforward. But what does a great circle path look like plotted on a hypothetical flat Earth? Here are a few:

Equator on flat Earth

The equator.

Great circle passing through London and Sydney

Great circle passing through London and Sydney.

Great circle passing through Rome and McMurdo Station, Antarctica

Great circle passing through Rome and McMurdo Station, Antarctica.

As you can see, great circle paths are distorted and misshapen when plotted on a flat Earth. If you follow a straight line across the surface of the Earth as given by inertial navigation systems there’s no obvious reason why you would end up tracing any of these paths, or why you would measure the same distance travelled (40,000 km) over all three paths when they are significantly different sizes on this map. And then consider this one:

Great circle passing through London and the North Pole

Great circle passing through London and the North Pole.

This circle passes through the north and south poles. If you travel on this great circle, then you have to go off one edge of the flat Earth and reappear on the other side. Which seems unlikely.

Travelling in a straight line and ending up where you started makes the most sense if the Earth is a globe.

References:

[1] “MythBusters Episode 173: Walk a Straight Line”, MythBuster Results, https://mythresults.com/walk-a-straight-line (accessed 2019-08-20).

[2] “Inertial Navigation System (INS)”, Skybrary, https://www.skybrary.aero/index.php/Inertial_Navigation_System_(INS) (accessed 2019-08-20).