Month: July 2020

44. Magnetic striping

We’ve discussed continental drift and plate tectonics in Proof 22. Plate tectonics. There’s another aspect of plate tectonics that was mentioned in passing there, which deserves some further attention. Proof 22 stated:

But as technology advanced, detailed measurements of the sea floor were made beginning in the late 1940s, including the structures, rock types, and importantly the magnetic properties of the rocks.

That last one, the “magnetic properties”, was the piece of evidence that really cemented continental drift as a real thing.

We pick up the history in 1947, when research expeditions led by American oceanographer Maurice Ewing established the existence of a long ridge running roughly north-south down the middle of the Atlantic Ocean. They also found that the crust beneath the ocean was thinner than that beneath the continents, and that the rocks (below the seafloor sediment) were basalts, rather than the granites predominantly found on continents. There was something peculiar about the Earth’s crust around these mid-ocean ridges. And over the next few years, more ridges were found in other oceans, revealing a network of the structures around the globe. The system of mid-ocean ridges had been discovered, but nobody yet had an explanation for it.

Meanwhile, from 1957, the Russian-American oceanographer Victor Vacquier took World War II surplus aerial magnetometers that had been used to detect submerged submarines from reconnaissance aircraft, and adapted them for use in submarines to examine the magnetic properties of the sea floor. It was well known that basalt contained the mineral magnetite, which is rich in iron and can be strongly magnetised.

What Vacquier found was unexpected and astonishing. In a survey of the Mendocino Fault area off the coast of San Francisco, Vacquier discovered that the sea floor basalt was not uniformly magnetised, but rather showed a distinctive and striking pattern. The magnetism appeared to be relatively constant along north-south lines, but to vary rapidly along the east-west direction, causing “stripes” of magnetism running north-south.[1]

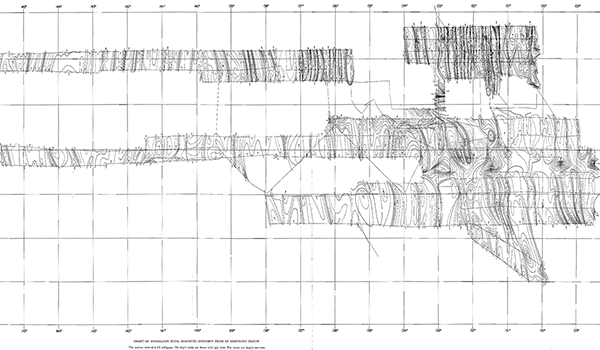
Magnetic field measurements on the sea floor near Mendocino Fault

Map of magnetic field measurements on the sea floor near Mendocino Fault, showing strong north-south striping of the magnetic field. (Figure reproduced from [1].)

Follow up observations showed that the stripes were not localised, but extended over large regions of the ocean.[2][3].

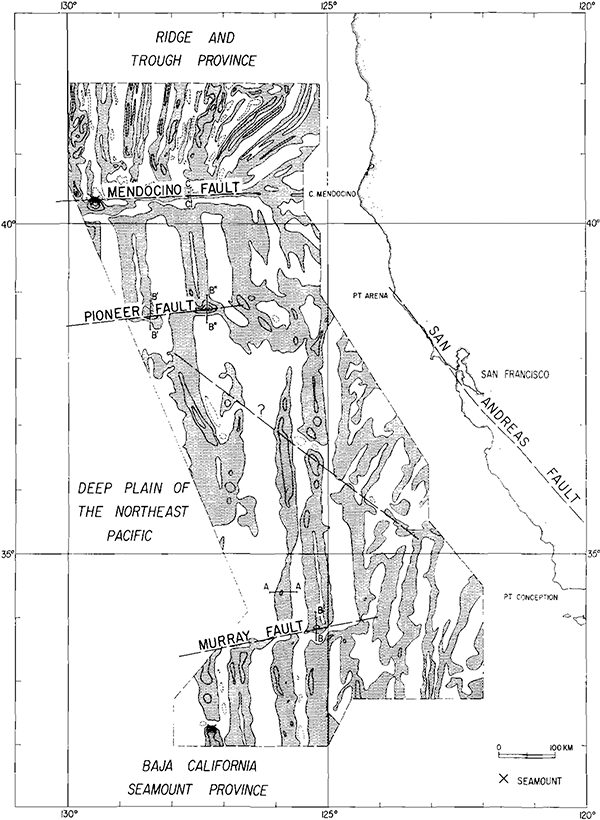
Magnetic anomalies on the sea floor off California

Map of magnetic anomalies on the sea floor off California. Shaded areas are positive magnetic anomaly, unshaded areas are negative. (Figure reproduced from [2].)

In fact, these magnetic “zebra stripes” were present pretty much everywhere on the floor of every ocean. They weren’t always aligned north-south though – it turned out that they were aligned parallel to the mid-ocean ridges. The early discoverers of this odd phenomenon had no explanation for it.

Returning to the mid-ocean ridges, American oceanographer Bruce Heezen wrote a popular article in Scientific American in 1960 that informed readers of the recent discoveries of these enormous submarine geological features.[4] In the article, he speculated that perhaps the ridges were regions of upwelling material from deep within the Earth, and the sea floors were expanding outwards from the ridges. Heezen was not aware of any mechanism for regions of Earth’s crust to disappear, so he suggested that the Earth might slowly be expanding, through the creation of new crust at the mid-ocean ridges.

Although Heezen’s idea of an expanding Earth didn’t take hold, his idea of upwelling and expansion along the mid-ocean ridges was quickly combined with existing proposals (that Heezen had overlooked) that crust could be disappearing along the lines of deep ocean trenches, as parts of the Earth moved together and were subducted downwards. The American geologists Harry Hammond Hess and Robert S. Dietz independently synthesised the ideas into a coherent theory of continental drift, combining the hypotheses of seafloor spreading and ocean trench subduction to conclude that the Earth was not changing size, but rather it was fractured into crustal plates that slowly moved, spreading apart in some places, and colliding and subducting in others.[5][6]

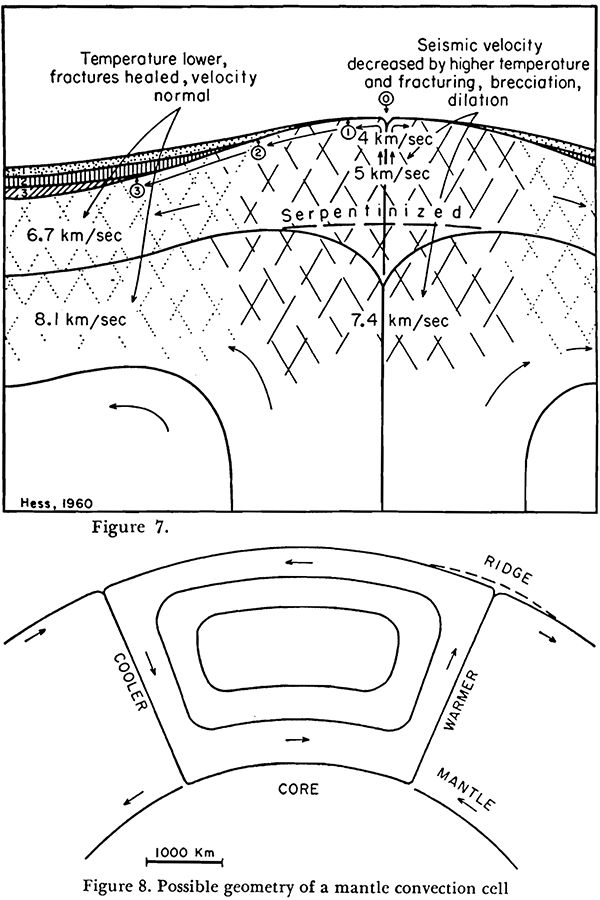
Proposed mantle convection by Hess

Earliest diagrams of proposed mantle convection cells causing continental drift, with upwelling at mid-ocean ridges causing seafloor spreading, by Harry Hammond Hess. Figure 7 (top) shows the detailed structure of a mid-ocean ridge, with measured seismic velocities (the speed of seismic waves in the rock) in various regions. Hess proposed that the observed lower speeds in the central and upper zones were caused by fracturing of the rock as it deforms during the upwelling, plus higher residual temperature of the upwelled material. Figure 8 (bottom) shows Hess’s proposed mantle convection cells. (Figures reproduced from [6].)

So by the 1960s, most of the observational pieces of this puzzle were in place. However, the unifying theory that would explain it all still required some synthesis, and acceptance of some unestablished hypotheses. This synthesis was again put together independently by two different groups of geologists: the Canadian Lawrence Morley, and the English Ph.D. student Frederick Vine and his supervisor Drummond Matthews. Morley wrote two papers and submitted them to Nature and the Journal of Geophysical Research in 1963, but both journals rejected his work as too speculative. Vine and Matthews thus received publication priority when Nature accepted their paper later in 1963.[7]

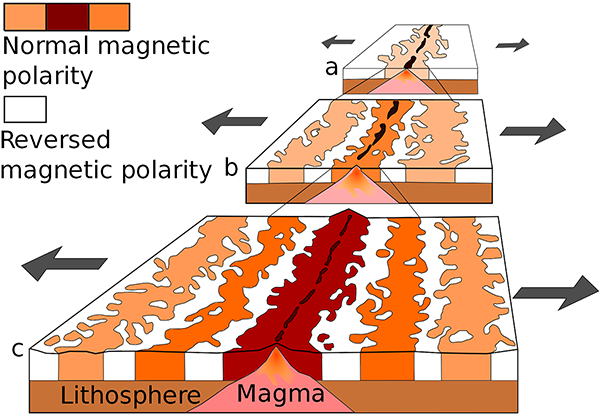
The geologists pointed out that if new rock was being created at the mid-ocean ridges and then spreading outwards, then the seafloor rocks should get progressively older the further away they are from the ridges. Each one of the magnetic zebra stripes running parallel to the ridges then corresponds to rocks of the same age. If, they conjectured, the rocks record the direction of the Earth’s magnetic field when they were formed, and for some reason the Earth’s magnetic field reversed direction periodically, that would explain the existence of the magnetic stripes.

Observed and modelled sea floor magnetic fields

Diagram by Vine and Matthews showing the observed magnetic field strength of the sea floor rocks measured across the Carlsberg Ridge in the Indian Ocean, showing positive and negative regions (solid lines), computed magnetic field strength under conventional (for the time) assumptions (dashed lines), and computed field strength assuming 20 km wide bands in which the Earth’s magnetic field has been reversed. The periodic field reversal matches the observed magnetism much better. (Figure reproduced from [7].)

As with Morley’s rejected papers, this paper was treated with scepticism initially, because it relied on two unproven conjectures: (1) that the rocks maintain magnetism aligned with the Earth;’s magnetic field at the time of solidification and, much more unbelievably, (2) that the Earth’s magnetic field direction reverses periodically. For some geologists, this was too speculative to be believe.

One test of Vine and Matthews’ seafloor spreading hypothesis would be to measure the age of the sea floor using some independent method. If the rocks were found to get progressively older the further away they are from the mid-ocean ridges, then that would be strong evidence in favour of the theory. As it happens, it’s possible to date the age of rocks formed from magma, using a method of radiometric dating known as potassium-argon (K-Ar) dating. Potassium is a fairly common element in rocks, and the isotope potassium-40 is radioactive, with a half-life of 1.248×109 years. Most of the potassium-40 decays to calcium-40 via beta decay (see Proof 29. Neutrino beams for a recap on beta decay), but just over 10% of it decays via electron capture to the inert gas argon-40. Argon is not present in newly solidified rock, but the argon produced by decaying potassium-40 is trapped within the crystal structure. Since the decay rate is known very precisely, we can use the measured ratio of potassium to argon in the rock to determine how long it has been since it formed, for timescales from several million to billions of years.

In the mid-1960s, oceanographers and geologists began drilling cores and taking basalt samples from the sea floor and measuring their ages.[8] And what they found matched the prediction from seafloor spreading: the youngest rocks were at the ridges and became progressively older towards the edges of the oceans.

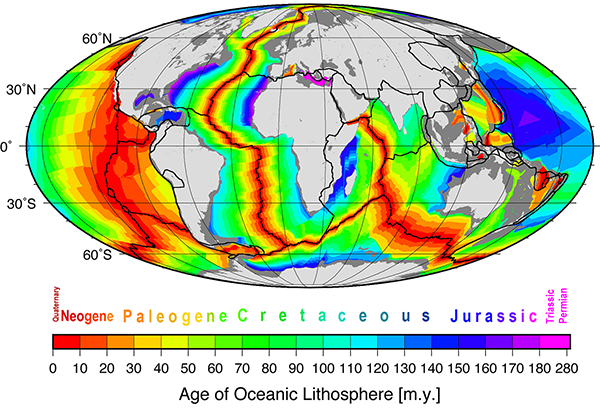
Age of oceanic crust

Diagram of the age of oceanic crust. The youngest rocks are red, and found along the mid-ocean ridges. Rocks are progressively older further away from the ridges. (Figure reproduced from [9].)

This was exactly what Vine and Matthews predicted. Belatedly, Morley also received his due credit for coming up with the same idea, and their proposal is now known as the Vine-Matthews-Morley hypothesis. The magnetic striping of the ocean floors is caused by the combination of the spreading of the ocean floors from the mid-ocean ridges, and the periodic reversal of Earth’s magnetic field.

Generation of magnetic striping

Generation of magnetic striping on the sea floor. As the sea floor spreads, and the Earth’s magnetic field reverses from time to time, stripes of different magnetic polarity are created and spread outwards. (Public domain image by the United States Geological Survey, from Wikimedia Commons.)

Odd reversals of magnetic fields in continental rocks had been noticed since 1906, when the French geologist Bernard Brunhes found that some volcanic rocks were magnetised in the opposite direction to the Earth’s magnetic field. In the 1920s, the Japanese geophysicist Motonori Matuyama noticed that all of the reversed rocks found by Brunhes and others since were older than the early Pleistocene epoch, around 750,000 years ago. He suggested that the Earth’s field may have changed direction around that time, but his proposal was largely ignored.

With the impetus provided by the seafloor spreading idea, geologists began measuring magnetic fields and ages of more rocks, and found that they matched up with the ages of the field reversals implied by the sea floor measurements. Progress was rapid and the geological community turned around and developed and adopted the whole theory of plate tectonics within just a few years. By the end of the 1960s, what had been ridiculed less than a decade earlier was mainstream, brought to that status by the confluence of multiple lines of observational evidence.

It had been established that the Earth’s magnetic field must reverse direction with periods of a few tens of thousands to millions of years. The remaining question was how?

Up until the development of plate tectonics, the origin of the Earth’s magnetic field had been a mystery. Albert Einstein even weighed in, suggesting that it might be caused by an imbalance in electrical charge between electrons and protons. But plate tectonics not only raised the question – it also suggested the answer.

The core of the Earth was known to be mostly metallic (see Proof 43. The Schiehallion experiment). If there are convection currents in the mantle, then heat differentials at the boundary should also cause convection within the core. The convecting metal induces electrical currents, which in turn produce a magnetic field. In short, the core of the Earth is an electrical dynamo. And because the outer core is liquid, the currents are unstable. Modern computer simulations of convection in the Earth’s core readily produce instabilities that act to flip the polarity of the magnetic field at irregular intervals – exactly as observed in the record of magnetic striped sea floor rocks.

Simulations of magnetic field reversal in Earth's core

Computer simulations of convection currents in the Earth’s core and resulting magnetic field lines. Blue indicates north magnetic polarity, yellow south. The left image indicates Earth in a stable state, with a magnetic north pole at the top and a south at the bottom. The middle image is during an instability, with north and south intermingled and chaotic. The right image is after the unstable period, with the north and south poles now flipped. (Public domain images by NASA, from Wikimedia Commons.)

So we have a fully coherent and self-consistent theory that explains the observations of magnetic striping, along with many other features of the Earth’s geophysics. It involves several interlocking components: convection in the metallic core producing electric currents that generate a magnetic field that is unstable over millions of years and flips polarity at irregular intervals; convection in the mantle producing upwellings of material along mid-ocean ridges, leading to seafloor spreading and continental drift; rocks that record both their age and the direction and strength of the Earth’s magnetic field when they are formed, leading to magnetic striping on the ocean beds.

Of course, this only holds together and makes sense on a spherical Earth. We’ve already seen in Proof 8. Earth’s magnetic field, that simply generating the shape of the planet’s magnetic field only works on a spherical Earth, and is an inexplicable mystery on a flat Earth model. It would be even more difficult to explain the irregular reversal of polarity of the magnetic field without a spherical core dynamo system. And plate tectonics just doesn’t work on a flat Earth either (Proof 22. Plate tectonics). Combining the fact that neither of these explanations work on a flat Earth, there is no explanation for the observed magnetic striping of the sea floors either. So magnetic striping provides another proof that the Earth is a globe.

References:

[1] Vacquier, V., Raff, A.D., Warren, R.E. “Horizontal displacements in the floor of the northeastern Pacific Ocean”. Geological Society of America Bulletin, 72(8), p.1251-1258, 1961. https://doi.org/10.1130/0016-7606(1961)72[1251:HDITFO]2.0.CO;2

[2] Mason, R.G. Raff, A.D. “Magnetic survey off the west coast of North America, 32 N. latitude to 42 N. Latitude”. Geological Society of America Bulletin, 72(8), p.1259-1265, 1961. https://doi.org/10.1130/0016-7606(1961)72[1259:MSOTWC]2.0.CO;2

[3] Raff, A.D. Mason, R.G. “Magnetic survey off the west coast of North America, 40 N. latitude to 52 N. Latitude”. Geological Society of America Bulletin, 72(8), p.1267-1270, 1961. https://doi.org/10.1130/0016-7606(1961)72[1267:MSOTWC]2.0.CO;2

[4] Heezen, B.C. “The rift in the ocean floor”. Scientific American, 203(4), p.98-114, 1960. https://www.jstor.org/stable/24940661

[5] Dietz, R.S. “Continent and ocean basin evolution by spreading of the sea floor”. Nature, 190(4779), p.854-857, 1961. https://doi.org/10.1038%2F190854a0

[6] Hess, H.H. “History of Ocean Basins: Geological Society of America Bulletin”. Petrologic Studies: A Volume to Honour AF Buddington, p.559-620, 1962. https://doi.org/10.1130/Petrologic.1962.599

[7] Vine, F.J. Matthews, D.H. “Magnetic anomalies over oceanic ridges”. Nature, 199(4897), p.947-949, 1963. https://doi.org/10.1038/199947a0

[8] Orowan, E., Ewing, M., Le Pichon, X. Langseth, M.G. “Age of the ocean floor”. Science, 154(3747), p.413-416, 1966. https://doi.org/10.1126/science.154.3747.413

[9] Müller, R.D., Sdrolias, M., Gaina, C. Roest, W.R. “Age, spreading rates, and spreading asymmetry of the world’s ocean crust”. Geochemistry, Geophysics, Geosystems, 9(4), 2008. https://doi.org/10.1029/2007GC001743

43. The Schiehallion experiment

The Ancients had the technology and cleverness to work out the shape of the Earth and its diameter (see 2. Eratosthenes’ measurement). However, they had no reliable method to measure the mass of the Earth, or equivalently its density, which gives the mass once you know the volume. You could assume that the Earth has a density similar to rock throughout, but there was no way of knowing if that was correct.

In fact we had no measurement of the density or mass of the Earth until the 18th century. Perhaps surprisingly, there wasn’t even any observational evidence to decide whether the Earth was actually a solid object, or a hollow shell with a relatively thin solid crust. As late as 1692 the prominent scientist Edmond Halley proposed that the Earth might be composed of a spherical shell around 800 km thick, with two smaller shells inside it and a solid core, all separated by a “luminous” atmosphere (which could escape and cause the aurora borealis).

Edmond Halley's hollow Earth model

Structure of the Earth as proposed by Edmond Halley in 1692, with solid shells (brown) separated by a luminous atmosphere, shown in cross section.

In his 1687 publication of Philosophiæ Naturalis Principia Mathematica, Isaac Newton presented his theory of universal gravitation. Although this provided explicit equations relating the physical properties of gravitational force, mass, and size, for the cases of astronomical objects there were still more than one unknown value, so the equations could not be solved to determine the absolute masses or densities of planets. The best astronomers could do was determine ratios of densities of one planet to another.

But Newton not only proposed his formulation of gravity as a theoretical construct – he also suggested a possible experiment that could be done to test it. As observed by common experience, objects near the surface of the Earth fall downwards – they are attracted towards the centre of the Earth (more precisely, the Earth’s centre of mass). But if the attractive force of gravity is generated by mass as per Newton’s formulation, then unusual concentrations of mass should change the direction of the gravitational pull a little.

We’ve already seen in Proof 24. “Gravitational acceleration variation” that the strength of Earth’s gravitational pull varies across the Earth’s surface due to differences in altitude and density within the Earth. Now imagine a large concentration of mass on the surface of the Earth. If Newton is correct, then such a mass should pull things towards it. The attraction to the centre of the Earth is much stronger, so the direction of the overall gravitational pull should still be almost downwards, but there should be a slight deflection towards the large mass.

There are some convenient large masses on the surface of the Earth. We call them mountains. Newton conceived that one could go somewhere near a large mountain and measure the difference in angle between a plumb line (which indicates the direction of gravity, and is commonly called “vertical”) and a line pointing towards the Earth’s centre of mass (which does not have a well-defined name, since it is more difficult to measure and differs from a plumb line by an amount too small to be significant in engineering or construction – for the purposes of this proof only, I shall abbreviate it to “downwards”). However, Newton believed that any such difference would be too small to measure in practice. He writes in the Principia, Book 3: On the system of the world:

Hence a sphere of one foot in diameter, and of a like nature to the earth, would attract a small body placed near its surface with a force 20,000,000 times less than the earth would do if placed near its surface; but so small a force could produce no sensible effect. If two such spheres were distant but by 1/4 of an inch, they would not, even in spaces void of resistance, come together by the force of their mutual attraction in less than a month’s time; and lesser spheres will come together at a rate yet slower, namely in the proportion of their diameters. Nay, whole mountains will not be sufficient to produce any sensible effect. A mountain of an hemispherical figure, three miles high, and six broad, will not, by its attraction, draw the pendulum two minutes out of the true perpendicular; and it is only in the great bodies of the planets that these forces are to be perceived.[1]

Here is where Newton’s lack of experience as an experimentalist let him down. Two minutes of arc was already within the accuracies of stellar positions claimed by Tycho Brahe some 80 years earlier. If Newton had merely asked astronomers if they could measure a deflection of such a small size, they would likely have answered yes.

Tycho Brahe in his observatory at Uraniborg

Engraving of Tycho Brahe observing in his observatory at Uraniborg, Sweden. (Public domain image from Wikimedia Commons.)

If you can measure how big the deflection angle is with sufficient accuracy, then you can use that measurement to calculate the density of the Earth in terms of the density of the mountain:

ρE/ρM = (VM/VE) (rE/d)2 / tan θ

where:

ρE is the density of the Earth,
ρM is the density of the mountain,
VE is the volume of the Earth,
VM is the volume of the mountain,
rE is the radius of the Earth,
d is the horizontal distance from the centre of the mountain to the plumb bob, and
θ is the angle of deflection of the plumb line from “downwards”.

The volume of the mountain can be estimated from its size and shape, and the density may be assumed to be that of common types of rock. All the other values were known, leaving the as yet unknown density of the Earth as a function of the deflection angle.

Two French astronomers, Pierre Bouguer (who we met in 4. Airy’s coal pit experiment) and Charles Marie de La Condamine, were the first to attempt to make the measurement. In 1735 they led an expedition to South America to measure the length of an arc of one degree of latitude along a line of longitude near the equator. This was part of an experiment by the French Academy of Sciences—along with simultaneous expedition to Lapland to make a similar measurement near the North Pole—to measure the shape of the Earth. Not whether it was spherical; any difference between the measurements would show if it was more accurately a prolate or an oblate ellipsoid.

Bouguer and La Condamine spent ten years on their expedition, making many other physical, geographical, biological, and ethnographical studies. One experiment they tried in 1738 was measuring the deflection of a plumb bob near the 6263 metre high volcano Chimborazo, in modern day Ecuador.

Chimborazo in Ecuador

The volcano Chimborazo in Ecuador. (Creative Commons Attribution 2.0 image by David Ceballos, from Flickr.)

They climbed to an altitude of 4680 m on one flank of the mountain and 4340 m on the other side, battling harsh weather to take the two measurements. Taking two measurements on opposite sides of the mountain allows a subtraction to remove sources of error in locating the “downwards” direction, leaving behind the difference in angle between the two plumb bob directions, which is twice the desired deflection. Bouguer and La Condamine measured a deflection of 8 seconds of arc, however they considered the circumstances so difficult as to render it unreliable. But they did state that this measurement gave a large value for the Earth’s density, thus disproving the hypothesis that the Earth was hollow.

A more precise measurement of the gravitational deflection of a mountain had to wait until 1772, when Astronomer Royal Nevil Maskelyne made a proposal to repeat the experiment to the Royal Society of London.[2] The Society approved, and appointed the quaintly named Committee of Attraction to ponder the proposal. The committee (counting Joseph Banks and Benjamin Franklin among its members) despatched astronomer and surveyor Charles Mason (of Mason-Dixon line fame) to find a suitable mountain. He came back with Schiehallion, a 1083 m peak in central Scotland.

Schiehallion in Scotland

Schiehallion in central Scotland. (Creative Commons Attribution 3.0 Unported image by Wikipedia user Andrew2606, from Wikimedia Commons.)

Schiehallion had several advantages for the measurement. It’s conveniently located for a British expedition. It’s an isolated peak, with no other mountains nearby that could substantially complicate the effects of gravity in the region. It has a very symmetrical shape, making it easy to estimate the volume with some accuracy. And the northern and southern slopes are very steep, which means that by doing the experiment on those sides, the plumb bob can be positioned relatively close to the centre of mass of the mountain, increasing the deflection and making it easier to measure.

Maskelyne himself led the expedition, taking temporary leave from his post as Astronomer Royal. The party built temporary observatories on the northern and southern flanks of Schiehallion, from which they made frequent observations of overhead stars to determine the zenith line (marking the “downwards” direction), so they could compare it to the direction of the hanging plumb line. Maskelyne and his team spent 6 weeks at the southern observatory, followed by 10.5 weeks at the northern one, battling inclement weather to take the required number of observations.[3]

Map of Schiehallion and surrounds

Map of Schiehallion and surrounds. The mountain forms a short ridge running approximately east-west. The positions of the north and south observatories can be seen. (Reproduced from [6].)

Maskelyne had calculated that if the Earth as a whole had the same density as the mountain (i.e. that of quartzite rock), then they should have observed a deflection of the plumb line relative to “downwards” of 20.9 seconds of arc. Preliminary calculations showed a deflection of about half that, meaning the Earth was roughly twice as dense as the mountain.

To mark the successful conclusion of the observations, the expedition celebrated with a rollicking good party. Plenty of alcohol was imbibed (quite possibly Scotch whisky). In the revelry, unfortunately someone accidentally set fire to the northern observatory and it burnt to the ground. The fire claimed the violin of one Duncan Robertson, a junior member of the expedition who had helped to pass the long cold nights of observation by entertaining the other members with his playing. Later, a grateful Maskelyne sent Robertson a replacement violin – not just any violin, but one made by the master craftsman Antonio Stradivari.[4][5]

The mathematician and surveyor Charles Hutton was charged with doing the detailed calculations of the result. He published them in a mammoth 100-page paper in 1778.[6] His final conclusion was that the density of the Earth was 1.8 times the density of the quartzite in Schiehallion, or about 4.5 g/cm3. Since this was so much higher than the densities of various types of rock (typically between 2 and 3 g/cm3), Hutton concluded (correctly) that much of the core of the Earth must be metal, and he calculated that about 65% of the Earth’s diameter must be a metallic core (a little higher than current measurements of 55%).

Hutton's conclusions on the structure of Earth and density of planets

Extract of Hutton’s paper, where he states that roughly 2/3 of the diameter of the Earth must be metallic to account for the measured density. This page also shows Hutton’s calculations of the densities of solar system bodies. (Reproduced from [6].)

This was the very first time that we had any estimate of the density/mass of the Earth, and Hutton also used it to calculate the densities of the Sun, the Moon, and the planets (out to Saturn) based on their known astronomical properties, mostly to within about 20% of the modern values. So the Schiehallion experiment was groundbreaking and significantly increased our fundamental understanding of the Earth and the solar system.

Later experiments confirmed the general nature of the result and refined the figures for the density and structure of the Earth. In particular, Henry Cavendish—a chemist who 20 years earlier had discovered the elemental nature of hydrogen and made several other discoveries about air and elemental gases—turned his attention to physics and performed what has become known as the Cavendish experiment in 1797-98. He constructed a finely balanced mechanism with which he could measure the tiny gravitational attractive force between two balls of lead, which allowed the measurement of the (then unknown) value of Newton’s gravitational constant. Knowing this value, it becomes possible to directly plug in values for the size of the Earth and the acceleration due to gravity and determine the mass of the Earth. Cavendish’s result was accurate to about 1%, confirming Hutton’s conclusion that the Earth must have a core denser than rock. And then in the 20th century, seismology allowed us to confirm the existence of discrete layers within the Earth, with the central core made primarily of metal (a story for a future Proof).

Drawing of Henry Cavendish

Drawing of Henry Cavendish. (Creative Commons Attribution 4.0 International image by the Wellcome Collection of the British Library, from Wikimedia Commons.)

Of course, the conclusions of the Schiehallion experiment—consistent with later experiments using independent methods—depend on the fact that the Earth is very close to spherical, and the fact that gravity works as Newton said (disregarding the later refinement by Einstein, which is not significant here). One of the more popular Flat Earth models assumes that gravity does not even exist as a force, and that objects “fall” to Earth because the Flat Earth is actually accelerating upwards. In such a model, objects always fall directly “downwards” and there is no deflection caused by large masses such as mountains. The Schiehallion experiment directly and simply disproves this Flat Earth model.

If we suppose that a Flat Earth somehow manages to exist with Newtonian gravity (in itself virtually impossible, see 13. Hydrostatic equilibrium), we could posit something like the 859 km thick flat disc mentioned in 34. Earth’s internal heat. Firstly, Newtonian gravity on such a disc would not always pull perpendicular to the ground – inhabitants near the circumference would be pulled at a substantial angle towards the centre of the disc. Ignoring this, if you managed to do the Schiehallion experiment (say at the North Pole), the distance rE in the equation would be effectively 430 km (the distance to the centre of mass of the disc) rather than the radius of the spherical Earth, 6378 km. This should make the observed deflection angle approximately (6378/430)2 = 220 times smaller! Then the observed deflections would imply that the density of the Earth is 220 times higher, or around 990 g/cm3, about 6 times as dense as the core of the Sun. Which is then inconsistent with the assumed density being the same as the spherical Earth (among other problems).

On the other hand, if we allow the density to be a free parameter, we can solve the gravitational and geometric equations simultaneously to derive the thickness of the Flat Earth disc in a “consistent” manner. This produces a thickness of 3020 km, and a density of 92 g/cm3. Which is over 4 times as dense as osmium, the densest substance at non-stellar pressures. So we’ve shown that the Schiehallion experiment proves that this “Newtonian Flat Earth” model cannot possibly be composed of any known material.

Basically, the observations of the Schiehallion experiment cannot be made consistent with a flat Earth, thus providing evidence that the Earth is a globe.

References:

[1] Newton, I. Philosophiae Naturalis Principia Mathematica (1687). Trans. Andrew Motte, 1729.

[2] Maskelyne, N. “A proposal for measuring the attraction of some hill in this Kingdom”. Philosophical Transactions of the Royal Society, 65, p. 495-499, 1772. https://doi.org/10.1098/rstl.1775.0049

[3]. Sillitto, R.M. “Maskelyne on Schiehallion: A Lecture to The Royal Philosophical Society of Glasgow”. 1990. http://www.sillittopages.co.uk/schie/schie90.html

[4] Davies, R. D. “A Commemoration of Maskelyne at Schiehallion”. Quarterly Journal of the Royal Astronomical Society, 26, p. 289, 1985. https://ui.adsabs.harvard.edu/abs/1985QJRAS..26..289D

[5] Danson, E. Weighing the World. Oxford University Press, 2005. ISBN 978-0-19-518169-2.

[6] Hutton, C. “An Account of the Calculations made from the Survey and Measures taken at Schehallien, in order to ascertain the mean Density of the Earth”. Philosophical Transactions of the Royal Society. 68, p. 689-788, 1778. https://doi.org/10.1098/rstl.1778.0034