geophysics – 100 Proofs that the Earth is a Globe

44. Magnetic striping

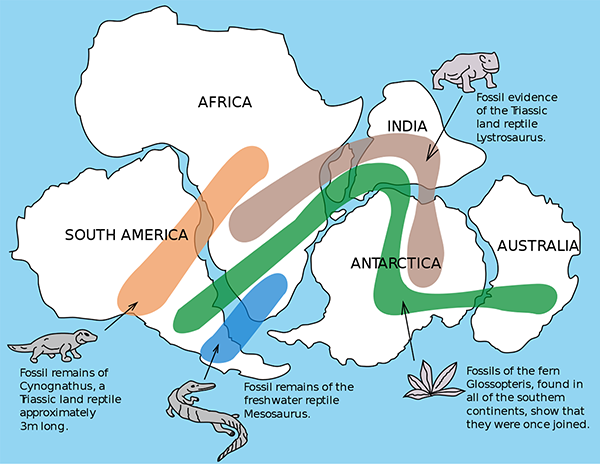
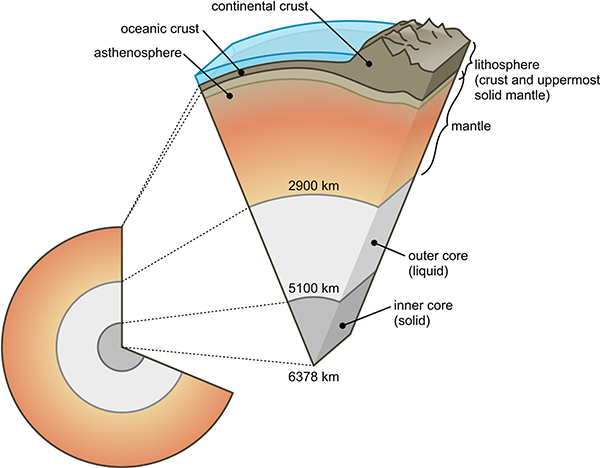
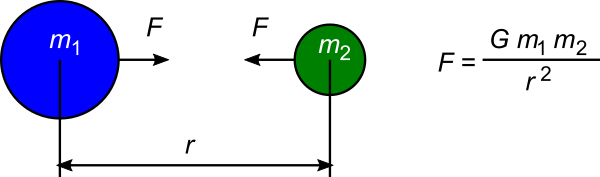
We’ve discussed continental drift and plate tectonics in Proof 22. Plate tectonics. There’s another aspect of plate tectonics that was mentioned in passing there, which deserves some further attention. Proof 22 stated:

But as technology advanced, detailed measurements of the sea floor were made beginning in the late 1940s, including the structures, rock types, and importantly the magnetic properties of the rocks.

That last one, the “magnetic properties”, was the piece of evidence that really cemented continental drift as a real thing.

We pick up the history in 1947, when research expeditions led by American oceanographer Maurice Ewing established the existence of a long ridge running roughly north-south down the middle of the Atlantic Ocean. They also found that the crust beneath the ocean was thinner than that beneath the continents, and that the rocks (below the seafloor sediment) were basalts, rather than the granites predominantly found on continents. There was something peculiar about the Earth’s crust around these mid-ocean ridges. And over the next few years, more ridges were found in other oceans, revealing a network of the structures around the globe. The system of mid-ocean ridges had been discovered, but nobody yet had an explanation for it.

Meanwhile, from 1957, the Russian-American oceanographer Victor Vacquier took World War II surplus aerial magnetometers that had been used to detect submerged submarines from reconnaissance aircraft, and adapted them for use in submarines to examine the magnetic properties of the sea floor. It was well known that basalt contained the mineral magnetite, which is rich in iron and can be strongly magnetised.

What Vacquier found was unexpected and astonishing. In a survey of the Mendocino Fault area off the coast of San Francisco, Vacquier discovered that the sea floor basalt was not uniformly magnetised, but rather showed a distinctive and striking pattern. The magnetism appeared to be relatively constant along north-south lines, but to vary rapidly along the east-west direction, causing “stripes” of magnetism running north-south.[1]

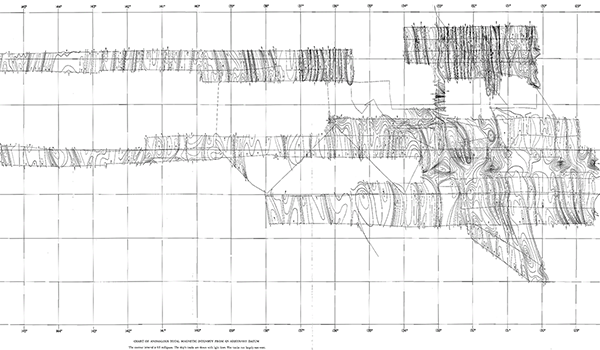
Magnetic field measurements on the sea floor near Mendocino Fault

Map of magnetic field measurements on the sea floor near Mendocino Fault, showing strong north-south striping of the magnetic field. (Figure reproduced from [1].)

Follow up observations showed that the stripes were not localised, but extended over large regions of the ocean.[2][3].

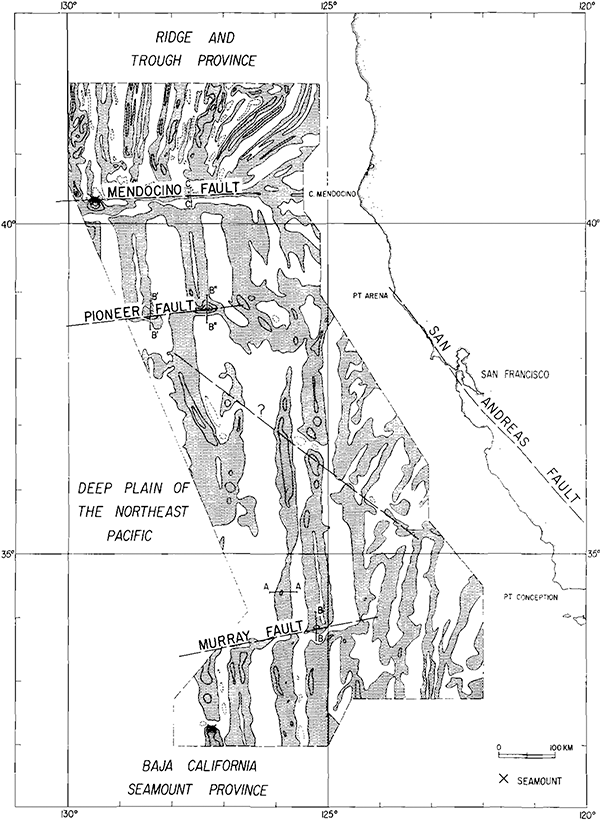
Magnetic anomalies on the sea floor off California

Map of magnetic anomalies on the sea floor off California. Shaded areas are positive magnetic anomaly, unshaded areas are negative. (Figure reproduced from [2].)

In fact, these magnetic “zebra stripes” were present pretty much everywhere on the floor of every ocean. They weren’t always aligned north-south though – it turned out that they were aligned parallel to the mid-ocean ridges. The early discoverers of this odd phenomenon had no explanation for it.

Returning to the mid-ocean ridges, American oceanographer Bruce Heezen wrote a popular article in Scientific American in 1960 that informed readers of the recent discoveries of these enormous submarine geological features.[4] In the article, he speculated that perhaps the ridges were regions of upwelling material from deep within the Earth, and the sea floors were expanding outwards from the ridges. Heezen was not aware of any mechanism for regions of Earth’s crust to disappear, so he suggested that the Earth might slowly be expanding, through the creation of new crust at the mid-ocean ridges.

Although Heezen’s idea of an expanding Earth didn’t take hold, his idea of upwelling and expansion along the mid-ocean ridges was quickly combined with existing proposals (that Heezen had overlooked) that crust could be disappearing along the lines of deep ocean trenches, as parts of the Earth moved together and were subducted downwards. The American geologists Harry Hammond Hess and Robert S. Dietz independently synthesised the ideas into a coherent theory of continental drift, combining the hypotheses of seafloor spreading and ocean trench subduction to conclude that the Earth was not changing size, but rather it was fractured into crustal plates that slowly moved, spreading apart in some places, and colliding and subducting in others.[5][6]

Proposed mantle convection by Hess

Earliest diagrams of proposed mantle convection cells causing continental drift, with upwelling at mid-ocean ridges causing seafloor spreading, by Harry Hammond Hess. Figure 7 (top) shows the detailed structure of a mid-ocean ridge, with measured seismic velocities (the speed of seismic waves in the rock) in various regions. Hess proposed that the observed lower speeds in the central and upper zones were caused by fracturing of the rock as it deforms during the upwelling, plus higher residual temperature of the upwelled material. Figure 8 (bottom) shows Hess’s proposed mantle convection cells. (Figures reproduced from [6].)

So by the 1960s, most of the observational pieces of this puzzle were in place. However, the unifying theory that would explain it all still required some synthesis, and acceptance of some unestablished hypotheses. This synthesis was again put together independently by two different groups of geologists: the Canadian Lawrence Morley, and the English Ph.D. student Frederick Vine and his supervisor Drummond Matthews. Morley wrote two papers and submitted them to Nature and the Journal of Geophysical Research in 1963, but both journals rejected his work as too speculative. Vine and Matthews thus received publication priority when Nature accepted their paper later in 1963.[7]

The geologists pointed out that if new rock was being created at the mid-ocean ridges and then spreading outwards, then the seafloor rocks should get progressively older the further away they are from the ridges. Each one of the magnetic zebra stripes running parallel to the ridges then corresponds to rocks of the same age. If, they conjectured, the rocks record the direction of the Earth’s magnetic field when they were formed, and for some reason the Earth’s magnetic field reversed direction periodically, that would explain the existence of the magnetic stripes.

Observed and modelled sea floor magnetic fields

Diagram by Vine and Matthews showing the observed magnetic field strength of the sea floor rocks measured across the Carlsberg Ridge in the Indian Ocean, showing positive and negative regions (solid lines), computed magnetic field strength under conventional (for the time) assumptions (dashed lines), and computed field strength assuming 20 km wide bands in which the Earth’s magnetic field has been reversed. The periodic field reversal matches the observed magnetism much better. (Figure reproduced from [7].)

As with Morley’s rejected papers, this paper was treated with scepticism initially, because it relied on two unproven conjectures: (1) that the rocks maintain magnetism aligned with the Earth;’s magnetic field at the time of solidification and, much more unbelievably, (2) that the Earth’s magnetic field direction reverses periodically. For some geologists, this was too speculative to be believe.

One test of Vine and Matthews’ seafloor spreading hypothesis would be to measure the age of the sea floor using some independent method. If the rocks were found to get progressively older the further away they are from the mid-ocean ridges, then that would be strong evidence in favour of the theory. As it happens, it’s possible to date the age of rocks formed from magma, using a method of radiometric dating known as potassium-argon (K-Ar) dating. Potassium is a fairly common element in rocks, and the isotope potassium-40 is radioactive, with a half-life of 1.248×10⁹ years. Most of the potassium-40 decays to calcium-40 via beta decay (see Proof 29. Neutrino beams for a recap on beta decay), but just over 10% of it decays via electron capture to the inert gas argon-40. Argon is not present in newly solidified rock, but the argon produced by decaying potassium-40 is trapped within the crystal structure. Since the decay rate is known very precisely, we can use the measured ratio of potassium to argon in the rock to determine how long it has been since it formed, for timescales from several million to billions of years.

In the mid-1960s, oceanographers and geologists began drilling cores and taking basalt samples from the sea floor and measuring their ages.[8] And what they found matched the prediction from seafloor spreading: the youngest rocks were at the ridges and became progressively older towards the edges of the oceans.

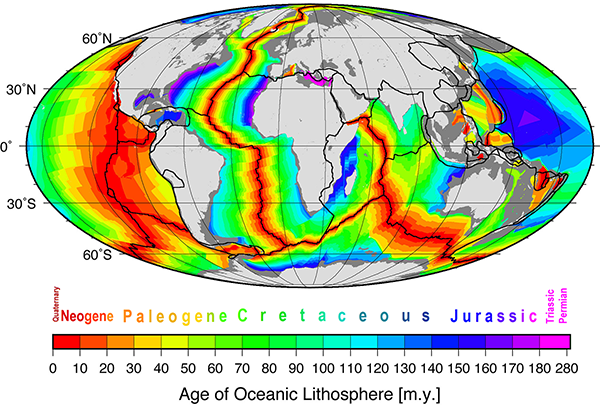
Age of oceanic crust

Diagram of the age of oceanic crust. The youngest rocks are red, and found along the mid-ocean ridges. Rocks are progressively older further away from the ridges. (Figure reproduced from [9].)

This was exactly what Vine and Matthews predicted. Belatedly, Morley also received his due credit for coming up with the same idea, and their proposal is now known as the Vine-Matthews-Morley hypothesis. The magnetic striping of the ocean floors is caused by the combination of the spreading of the ocean floors from the mid-ocean ridges, and the periodic reversal of Earth’s magnetic field.

Generation of magnetic striping on the sea floor. As the sea floor spreads, and the Earth’s magnetic field reverses from time to time, stripes of different magnetic polarity are created and spread outwards. (Public domain image by the United States Geological Survey, from Wikimedia Commons.)

Odd reversals of magnetic fields in continental rocks had been noticed since 1906, when the French geologist Bernard Brunhes found that some volcanic rocks were magnetised in the opposite direction to the Earth’s magnetic field. In the 1920s, the Japanese geophysicist Motonori Matuyama noticed that all of the reversed rocks found by Brunhes and others since were older than the early Pleistocene epoch, around 750,000 years ago. He suggested that the Earth’s field may have changed direction around that time, but his proposal was largely ignored.

With the impetus provided by the seafloor spreading idea, geologists began measuring magnetic fields and ages of more rocks, and found that they matched up with the ages of the field reversals implied by the sea floor measurements. Progress was rapid and the geological community turned around and developed and adopted the whole theory of plate tectonics within just a few years. By the end of the 1960s, what had been ridiculed less than a decade earlier was mainstream, brought to that status by the confluence of multiple lines of observational evidence.

It had been established that the Earth’s magnetic field must reverse direction with periods of a few tens of thousands to millions of years. The remaining question was how?

Up until the development of plate tectonics, the origin of the Earth’s magnetic field had been a mystery. Albert Einstein even weighed in, suggesting that it might be caused by an imbalance in electrical charge between electrons and protons. But plate tectonics not only raised the question – it also suggested the answer.

The core of the Earth was known to be mostly metallic (see Proof 43. The Schiehallion experiment). If there are convection currents in the mantle, then heat differentials at the boundary should also cause convection within the core. The convecting metal induces electrical currents, which in turn produce a magnetic field. In short, the core of the Earth is an electrical dynamo. And because the outer core is liquid, the currents are unstable. Modern computer simulations of convection in the Earth’s core readily produce instabilities that act to flip the polarity of the magnetic field at irregular intervals – exactly as observed in the record of magnetic striped sea floor rocks.

Computer simulations of convection currents in the Earth’s core and resulting magnetic field lines. Blue indicates north magnetic polarity, yellow south. The left image indicates Earth in a stable state, with a magnetic north pole at the top and a south at the bottom. The middle image is during an instability, with north and south intermingled and chaotic. The right image is after the unstable period, with the north and south poles now flipped. (Public domain images by NASA, from Wikimedia Commons.)

So we have a fully coherent and self-consistent theory that explains the observations of magnetic striping, along with many other features of the Earth’s geophysics. It involves several interlocking components: convection in the metallic core producing electric currents that generate a magnetic field that is unstable over millions of years and flips polarity at irregular intervals; convection in the mantle producing upwellings of material along mid-ocean ridges, leading to seafloor spreading and continental drift; rocks that record both their age and the direction and strength of the Earth’s magnetic field when they are formed, leading to magnetic striping on the ocean beds.

Of course, this only holds together and makes sense on a spherical Earth. We’ve already seen in Proof 8. Earth’s magnetic field, that simply generating the shape of the planet’s magnetic field only works on a spherical Earth, and is an inexplicable mystery on a flat Earth model. It would be even more difficult to explain the irregular reversal of polarity of the magnetic field without a spherical core dynamo system. And plate tectonics just doesn’t work on a flat Earth either (Proof 22. Plate tectonics). Combining the fact that neither of these explanations work on a flat Earth, there is no explanation for the observed magnetic striping of the sea floors either. So magnetic striping provides another proof that the Earth is a globe.

References:

[1] Vacquier, V., Raff, A.D., Warren, R.E. “Horizontal displacements in the floor of the northeastern Pacific Ocean”. Geological Society of America Bulletin, 72(8), p.1251-1258, 1961. https://doi.org/10.1130/0016-7606(1961)72[1251:HDITFO]2.0.CO;2

[2] Mason, R.G. Raff, A.D. “Magnetic survey off the west coast of North America, 32 N. latitude to 42 N. Latitude”. Geological Society of America Bulletin, 72(8), p.1259-1265, 1961. https://doi.org/10.1130/0016-7606(1961)72[1259:MSOTWC]2.0.CO;2

[3] Raff, A.D. Mason, R.G. “Magnetic survey off the west coast of North America, 40 N. latitude to 52 N. Latitude”. Geological Society of America Bulletin, 72(8), p.1267-1270, 1961. https://doi.org/10.1130/0016-7606(1961)72[1267:MSOTWC]2.0.CO;2

[4] Heezen, B.C. “The rift in the ocean floor”. Scientific American, 203(4), p.98-114, 1960. https://www.jstor.org/stable/24940661

[5] Dietz, R.S. “Continent and ocean basin evolution by spreading of the sea floor”. Nature, 190(4779), p.854-857, 1961. https://doi.org/10.1038%2F190854a0

[6] Hess, H.H. “History of Ocean Basins: Geological Society of America Bulletin”. Petrologic Studies: A Volume to Honour AF Buddington, p.559-620, 1962. https://doi.org/10.1130/Petrologic.1962.599

[7] Vine, F.J. Matthews, D.H. “Magnetic anomalies over oceanic ridges”. Nature, 199(4897), p.947-949, 1963. https://doi.org/10.1038/199947a0

[8] Orowan, E., Ewing, M., Le Pichon, X. Langseth, M.G. “Age of the ocean floor”. Science, 154(3747), p.413-416, 1966. https://doi.org/10.1126/science.154.3747.413

[9] Müller, R.D., Sdrolias, M., Gaina, C. Roest, W.R. “Age, spreading rates, and spreading asymmetry of the world’s ocean crust”. Geochemistry, Geophysics, Geosystems, 9(4), 2008. https://doi.org/10.1029/2007GC001743

34. Earth’s internal heat

Opening disclaimer: I’m going to be talking about “heat” a lot in this one. Formally, “heat” is defined as a process of energy flow, and not as an amount of thermal energy in a body. However to people who aren’t experts in thermodynamics (i.e. nearly everyone), “heat” is commonly understood as an “amount of hotness” or “amount of thermal energy”. To avoid the linguistic awkwardness of using the five-syllable phrase “thermal energy” in every single instance, I’m just going to use this colloquial meaning of “heat”. Even some of the papers I cite use “heat” in this colloquial sense. I’ve already done it in the title, which to be technically correct should be the more awkward and less pithy “Earth’s internal thermal energy”.

The interior of the Earth is hot. Miners know first hand that as you go deeper into the Earth, the temperature increases. The deepest mine on Earth is the TauTona gold mine in South Africa, reaching 3.9 kilometres below sea level. At this depth, the rock temperature is 60°C, and considerable cooling technology is required to bring the air temperature down to a level where the miners can survive. The Kola Superdeep Borehole in Russia reached a depth of 12.2 km, where it found the temperature to be 180°C.

Lava—molten rock—emerging from the Earth in Hawaii. (Public domain image by the United States Geological Survey, from Wikimedia Commons.)

Deeper in the Earth, the temperature gets hot enough to melt rock. The results are visible in the lava that emerges from volcanic eruptions. How did the interior of the Earth get that hot? And exactly how hot is it down there?

For many years, geologists have been measuring the amount of thermal energy flowing out of the Earth, at thousands of measuring stations across the planet. A 2013 paper analyses some 38,374 heat flow measurements across the globe to produce a map of the mean heat flow out of the Earth, shown below[1]:

Mean heat flow out of the Earth

Mean heat flow out of the Earth in milliwatts per square metre, as a function of location. (Figure reproduced from [1].)

From the map, you can see that most of Earth’s heat emerges at the mid-ocean ridges, deep underwater. This makes sense, as this is where rising plumes of magma from deep within the mantle are acting to bring new rock material to the crust. The coolest areas are generally geologically stable regions in the middle of tectonic plates.

Subterranean material (and heat) emerging from a hydrothermal vent on Eifuku Seamount, Marianas Trench Marine National Monument. (Public domain image by the United States National Oceanic and Atmospheric Administration, from Wikimedia Commons.)

Although the heat flow out of the Earth’s surface is of the order of milliwatts per square metre, the surface has a lot of square metres. The overall heat flow out of the Earth comes to a total of around 47 terawatts[2]. In contrast, the sun emits close to 4×10¹⁴ terawatts of energy in total, and the solar energy falling on the Earth’s surface is 1360 watts per square metre, over 10,000 times as much as the heat energy leaking out of the Earth itself. So the sun dominates Earth’s heating and weather systems by roughly that factor.

So the Earth generates some 47 TW of thermal power. Where does this huge amount of energy come from? To answer that, we need to go all the way back to when the Earth was formed, some 4.5 billion years ago.

Our sun formed from the gaseous and dusty material distributed throughout the Galaxy. This material is not distributed evenly, and where there is a denser concentration, gravity acts to draw in more material. As the material is pulled in, any small motions are amplified into an overall rotation. The result is an accretion disc, with matter spiralling into a growing mass at the centre. When the central concentration accumulates enough mass, the pressure ignites nuclear reactions and a star is born. Some of the leftover material continues to orbit the new star and forms smaller accretions that eventually become planets or smaller bodies.

The process of accreting matter generates thermal energy. Gravitational potential energy reduces as matter pulls closer together, and the resulting collisions between matter particles convert it into thermal energy, heating up the accumulating mass. Our Earth was born hot. As the matter settled into a solid body, the shrinking further heated the core through the Kelvin-Helmholtz mechanism. The total heat energy from the initial formation of the Earth dissipates only very slowly into space, and that process is still going on today, 4.5 billion years later.

It’s not known precisely how much of this primordial heat is left in Earth or how much flows out, but various different studies suggest it is somewhere in the range of 12-30 TW, roughly a quarter to two-thirds of Earth’s total measured heat flux[3]. So that’s not the only source of the heat energy flowing out of the Earth.

The other source of Earth’s internal heat is radioactive decay. Some of the matter in the primordial gas and dust cloud that formed the sun and planets was produced in the supernova explosions of previous generations of stars. These explosions produce atoms of radioactively unstable isotopes. Many of these decay relatively rapidly and are essentially gone by now. But some isotopes have very long half-lives, most importantly: potassium-40 (1.25 billion years), thorium-232 (14.05 billion years), uranium-235 (703.8 million years), and uranium-238 (4.47 billion years). These isotopes still exist in significant quantities inside the Earth, where they continue to decay, releasing energy.

We have a way of probing how much radioactive energy is released inside the Earth. The decay reactions produce neutrinos (which we’ve met before), and because they travel unhindered through the Earth these can be detected by neutrino observatories. These geoneutrinos have energy ranges that distinguish them from cosmic neutrino sources, and of course always emerge from underground. The observed decay rates from geoneutrinos correspond to a total radiothermal energy production of 10-30 TW, of the same order as the primordial heat flux. (The neutrinos themselves also carry away part of the energy from the radioactive decays, roughly 5 TW, but this is an additional component not deposited as thermal energy inside the Earth.)

Approximate radiothermal energy generated within the Earth, plotted as a function of time, from the formation of the Earth 4.5 billion years ago, to the present. The four main isotopes are plotted separately, and the total is shown as the dashed line. (Public domain figure adapted from data in [4], from Wikimedia Commons.)

To within the uncertainties, the sum of the estimated primordial and measured radiothermal energy fluxes is equal to the total measured 47 TW flux. So that’s good.

Once you know how much heat is being generated inside the Earth, you can start to apply heat transfer equations, knowing the thermodynamic properties of rock and iron, how much conduction and convection can be expected, and cross-referencing it with our knowledge of the physical state of these materials under different temperature and pressure conditions. There’s also additional information about the internal structure of the Earth that we get from seismology, but that’s a story for a future article. Putting it all together, you end up with a linked series of equations which you can solve to determine the temperature profile of the Earth as a function of depth.

Mean heat flow out of the Earth

Temperature profile of the Earth’s interior, from the surface (left) to the centre of the core (right). Temperature units are not marked on the vertical axis, but the temperature of the surface (bottom left corner) is approximately 300 K, and the inner core (IC, right) is around 7000 K. UM is upper mantle, LM lower mantle, OC outer core. The calculated temperature profile is the solid line. The two solid dots are fixed points constrained by known phase transitions of rock and iron – the slopes of the curves between them are governed by the thermodynamic equations. The dashed lines are various components of the constraining equations. (Figure reproduced from [5].)

The results are all self-consistent, with observations such as the temperature of the rock in deep mine shafts and the rate of detection of geoneutrinos, with structural constraints provided by seismology, and with the temperature constraints and known modes of heat flow from the core to the surface of the Earth.

That is, they’re all consistent assuming the Earth is a spherical body of rock and iron. If the Earth were flat, the thermal transport equations would need to be changed to reflect the different geometry. As a first approximation, assume the flat Earth is relatively thin (i.e. a cylinder with the radius larger than the height). We still measure the same amount of heat flux emerging from the Earth’s surface, so the same amount of heat has to be either (a) generated inside it, or (b) being input from some external energy source underneath the flat Earth. However geoneutrino energy ranges indicate that they come from radioactive decay of Earthly minerals, so it makes sense to conclude that radiothermal heating is significant.

If radioactive decay is producing heat within the bulk of the flat Earth, then half of the produced neutrinos will emerge from the underside, and thus be undetectable. So the total heat production should be double that deduced from neutrino observations, or somewhere in the range 20-60 TW. To produce twice the energy, you need twice the mass of the Earth. If the flat Earth is a disc with radius 20,000 km (the distance from the North Pole to the South Pole), then to have the same volume as the spherical Earth it would need to be 859 km thick. But we need twice as much mass to produce the observed thermal energy flux, so it should be approximately 1720 km thick. Some fraction of the geoneutrinos will escape from the sides of the cylinder of this thickness, which means we need to add more rock to produce a bit more energy to compensate, so the final result will be a bit thicker.

There’s no obvious reason to suppose that a flat Earth can’t be a bit over 1700 km thick, as opposed to any other thickness. With over twice as much mass as our spherical Earth, the surface gravity of this thermodynamically correct flat Earth would be over 2 Gs (i.e. twice the gravity we experience), which is obviously wrong, but then many flat Earth models deny Newton’s law of gravity anyway (because it causes so many problems for the model).

But just as in the spherical Earth model the observed geoneutrino flux only accounts for roughly half the observed surface heat flux. The other half could potentially come from primordial heat left over from the flat Earth’s formation – although as we’ve already seen, what we know about planetary formation precludes the formation of a flat Earth in the first place. The other option is (b) that the missing half of the energy is coming from some source underneath the flat Earth, heating it like a hotplate. What this source of extra energy is is mysterious. No flat Earth model that I’ve seen addresses this problem, let alone proposes a solution.

What’s more, if such a source of energy under the flat Earth existed, then it would most likely also radiate into space around the edges of the flat Earth, and have observable effects on the objects in the sky above us. What we’re left with, if we trust the sciences of radioactive decay and thermal energy transfer, is a strong constraint on the thickness of the flat Earth, plus a mysterious unspecified energy source underneath – neither of which are mentioned in standard flat Earth models.

References:

[1] Davies, J. H. “Global map of solid Earth surface heat flow”. Geochemistry, Geophysics, Geosystems, 14(10), p.4608-4622, 2013. https://doi.org/10.1002/ggge.20271

[2] Davies, J.H., Davies, D.R. “Earth’s surface heat flux”. Solid Earth, 1(1), p.5-24, 2010. https://doi.org/10.5194/se-1-5-2010

[3] Dye, S.T. “Geoneutrinos and the radioactive power of the Earth”. Reviews of Geophysics, 50(3), 2012. https://doi.org/10.1029/2012RG000400

[4] Arevalo Jr, R., McDonough, W.F., Luong, M. “The K/U ratio of the silicate Earth: Insights into mantle composition, structure and thermal evolution”. Earth and Planetary Science Letters, 278(3-4), p.361-369, 2009. https://doi.org/10.1016/j.epsl.2008.12.023

[5] Boehler, R. “Melting temperature of the Earth’s mantle and core: Earth’s thermal structure”. Annual Review of Earth and Planetary Sciences, 24(1), p.15-40, 1996. https://doi.org/10.1146/annurev.earth.24.1.15

22. Plate tectonics

Following the rediscovery of the New World by Europeans in the 15th century, the great seafaring nations of Europe rapidly mapped the eastern coastlines of the Americas. Demand for maps grew, not just of the New World, but of the Old as well. This made it possible for a young man (unfortunately women were shepherded into more domestic jobs) to seek his fortune as a mapmaker. One such man was Abraham Ortelius, who lived in Antwerp in the Duchy of Brabant (now part of Belgium).

Abraham Ortelius, painted by Peter Paul Rubens. (Public domain image from Wikimedia Commons.)

In 1547, at the age of 20, Ortelius began his career as a map engraver and illuminator. He travelled widely across Europe, and met cartographer and mapmaker Gerardus Mercator (15 years his senior, and whose map projection we met in 14. Map projections) in 1554. The two became friends and travelled together, reinforcing Ortelius’s passion for cartography, as well as the technical and scientific aspects of geography. Ortelius went on to produce and publish several maps of his own, culminating in his 1570 publication, Theatrum Orbis Terrarum (“Theatre of the Orb of the World”), now regarded as the first modern atlas of the world (as then known). Previously maps had been sold as individual sheets or bespoke sets customised to specific needs, but this was a curated collection intended to cover the entire known world in a consistent style. The Theatrum was wildly successful, running to 25 editions in seven languages by the time of Ortelius’s death in 1598.

World map plate from Theatrum Orbis Terrarum. (Public domain image from Wikimedia Commons.)

Being intimately familiar with his maps, Ortelius noticed a strange coincidence. In his publication Thesaurus Geographicus (“Geographical Treasury”) he wrote about the resemblance of the shapes of the east coast of the Americas to the west coasts of Europe and Africa across the Atlantic Ocean. He suggested that the Americas may have been “torn away from Europe and Africa … by earthquakes and floods. … The vestiges of the rupture reveal themselves, if someone brings forward a map of the world and considers carefully the coasts of the three.” This is the first known suggestion that the uncanny jigsaw-puzzle appearance of these coastlines might not be a coincidence, but rather a vestige of the continents actually having fitted together in the past.

Ortelius wasn’t the only one to make this observation and reach the same conclusion. Over the next few centuries, similar thoughts were proposed by geographers Theodor Christoph Lilienthal, Alexander von Humboldt, Antonio Snider-Pellegrini, Franklin Coxworthy, Roberto Mantovani, William Henry Pickering, Frank Bursley Taylor, and Eduard Suess. Suess even suggested (in 1885) that at some time in the past all of the Earth’s continents were joined in a single mass, which he gave the name “Gondwana”.

Illustration by Antonio Snider-Pellegrini, of his proposal that the Americas had once been adjacent to Europe and Africa. (Public domain image from Wikimedia Commons.)

Although many people had suggested that the continents had once been adjacent, nobody had produced any supporting evidence, nor any believable mechanism for how the continents could move. This changed in 1912, when the German meteorologist and polar scientist Alfred Wegener proposed the theory which he named continental drift. He began with the same observation of the jigsaw nature of the continent shapes, but then he applied the scientific method: he tested his hypothesis. He looked at the geology of coastal regions, examining the types of rocks, the geological structures, and the types of fossils found in places around the world. What he found were remarkable similarities in all of these features on opposite sides of the Atlantic Ocean, and in other locations around the world where he supposed that now-separate landmasses had once been in contact. This is exactly what you would expect to find if a long time ago the continents had been adjacent: plants and animals would have a range spanning across what would later split open and become an ocean, and geological features would be consistent across the divide as well[1].

Map of similar fossils of non-sea-going lifeforms found across landmasses, providing evidence that they were once joined. (Public domain image from Wikimedia Commons.)

In short, Wegener found and presented evidence in support of his hypothesis. He presented his theory, with the evidence he had gathered, in his 1915 book, Die Entstehung der Kontinente und Ozeane (“The Emergence of the Continents and Oceans”). He too proposed that all of the Earth’s continents were at one stage joined into a single landmass, which he named Pangaea (Greek for “all Earth”)[2].

But Wegener had two problems. Firstly, he still didn’t know how continents could possibly move. Secondly, he wasn’t a geologist, and so the establishment of geologists didn’t take him very seriously, to say the least. But as technology advanced, detailed measurements of the sea floor were made beginning in the late 1940s, including the structures, rock types, and importantly the magnetic properties of the rocks. Everything that mid-20th century geologists found was consistent with the existence of a large crack running down the middle of the Atlantic Ocean, where new rock material was welling up from beneath the ocean floor, and spreading outwards. They also found areas where the Earth’s crust was being squashed together, and either being thrust upwards like wrinkles in a tablecloth (such as the Himalayas mountain range), or plunged below the surface (such as along the west coast of the Americas).

Confronted with overwhelming evidence—which it should be pointed out was both consistent with many other observations, and also explained phenomena such as earthquakes and volcanoes better than older theories—the geological consensus quickly turned around[3]. The newly formulated theory of plate tectonics was as unstoppable as continental drift itself, and revolutionised our understanding of geology in the same way that evolution did for biology. Suddenly everything made sense.

The Earth, we now know, has a relatively thin, solid crust of rocks making up the continents and sea floors. Underneath this thin layer is a thick layer known as the mantle. The uppermost region of the mantle is solid and together with the crust forms what is known as the lithosphere. Below this region, most of the mantle is hot enough that the material there is visco-elastic, meaning it behaves like a thick goopy fluid, deforming and flowing under pressure. This viscous region of the mantle is known as the asthenosphere.

Diagram of the Earth’s layers. The lithosphere region is not to scale and would appear much thinner if drawn to scale. (Public domain image from Wikimedia Commons.)

Heat wells up from the more central regions of the Earth (generated by radioactive decay). Just like a boiling pot of water, this sets up convection currents in the asthenosphere, where the hot material flows upward, then sideways, then back down to form a loop. The sideways motion at the top of these convection cells is what carries the crust above, moving it slowly across the surface of the planet.

The Earth’s crust is broken into pieces, called tectonic plates, which fit together along their edges. Each plate is relatively rigid, but moves relative to the other plates. Plates move apart where the upwelling of the convection cells occurs, such as along the Mid-Atlantic Ridge (the previously mentioned crack in the Atlantic Ocean floor), and collide and subduct back down along other edges. At some plate boundaries the plates slide horizontally past one another. All of this motion causes earthquakes and volcanoes, which are mostly concentrated along the plate boundaries. The motion of the plates is slow, around 10-100 millimetres a year. This is too slow to notice over human history, except with high-tech equipment. GPS navigation and laser ranging systems can directly measure the movements of the continents relative to one another, confirming the speed of the motion.

The tectonic plates, then, are shell-like pieces of crust that fit together to form the spherical shape of the Earth’s surface. An equal amount of area is lost at subduction zones as is gained by spreading on sea-floors and in places such as Africa’s Rift Valley, keeping the Earth’s surface area constant. As the plates drift around, they don’t change in size or deform geometrically very much.

Earth's tectonic plates

Sketch of the major tectonic plates as they fit together to form the surface of the Earth.

All of this is consistent and supported by many independent pieces of evidence. Direct measurement shows that the continents are moving, so it’s really just a matter of explaining how. But the motions of the tectonic pates only make sense on a globe.

If the Earth were flat, then sure, you could conceivably have some sort of underlying structure that supports the same sort of convection cells and geological processes of spreading and subduction, leading to earthquakes and volcanoes, and so on. But look at the shapes of the tectonic plates.

Earth's tectonic plates on a flat Earth

Sketch of the major tectonic plates on a flat Earth.

Because of the distortions in the shape of the map relative to a globe, the tectonic plates need to change shape and size as they move across the surface. Not only that, but consider the Antarctic plate, which is a perfectly normal plate on the globe. On the typical Flat Earth model where Antarctica is a barrier of ice around the edge of the circle, the Antarctic plate is a ring. And when it moves, it not only has to deform in shape, but crust has to disappear off one side of the disc and appear on the other side.

So plate tectonics, the single most fundamental and important discovery in the entire field of geology, only makes sense because the Earth is a globe.

Notes:

[1] For readers interested in this particular aspect of continental drift, I’ve previously written about it at greater length in the annotation to this Irregular Webcomic! http://www.irregularwebcomic.net/1946.html

[2] Pangaea is now the accepted scientific term for the unified landmass when all the continents were joined. Eduard Suess’s Gondwana lives on as the name now used to refer to the conjoined southern continents before merging with the northern ones to form Pangaea.

[3] Alfred Wegener is often cited by various people in support of the idea that established science often laughs at revolutionary ideas proposed by outsiders, only for the outsider to later be vindicated. Often by people proposing outlandish or fringe science theories that defy not only scientific consensus but also the boundaries of logic and reason. What they fail to point out is that in all the history of science, Wegener is almost the only such case, whereas almost every other outsider proposing a radical theory is shown to be wrong. As Carl Sagan so eloquently put it in Broca’s Brain:

The fact that some geniuses were laughed at does not imply that all who are laughed at are geniuses. They laughed at Columbus, they laughed at Fulton, they laughed at the Wright brothers. But they also laughed at Bozo the Clown.

18. Polar motion

The Earth rotates around an axis, an imaginary straight line that all points not on the line move around in circles. The axis passes through the Earth’s North Pole and the South Pole. So the positions of the two Poles are defined by the position of the rotation axis.

The Earth’s North and South Poles are defined as the points where the axis of rotation passes through the surface of the planet. (Earth photo is a public domain image from NASA.)

Interestingly, the Earth’s rotation axis is not fixed – it moves slightly. This means that the Earth’s poles move.

The positions of the Earth’s poles can be determined by looking at the motions of the stars. As we’ve already seen, if you observe the positions of stars throughout a night, you will see that they rotate in the sky about a central point. The point on the Earth’s surface directly underneath the centre of rotation of the stars is one of the poles of the Earth.

Star trails above Little Hawk Lake in Canada. The northern hemisphere stars rotate around the North Celestial Pole (the point directly above the Earth’s North Pole). The bright spot in the centre is Polaris, the pole star. The circles are somewhat distorted in the upper corners of the photo because of the wide angle lens used. (Creative Commons Attribution 2.0 image by Dave Doe.)

Through the 19th century, astronomers were improving the precision of astronomical observations to the point where the movement of the Earth’s rotational poles needed to be accounted for in the positions of celestial objects. The motion of the poles was also beginning to affect navigation, because as the poles move, so does the grid system of latitude and longitude that ships rely on to reach their destinations and avoid navigational hazards. In 1899 the International Geodetic Association established a branch known as the International Latitude Service.

The fledgling International Latitude Service established a network of six observatories, all located close to latitude 39° 08’ north, spread around the world. The initial observatories were located in Gaithersburg, Maryland, USA; Cincinatti, Ohio, USA; Ukiah, California, USA; Mizusawa, Japan; Charjui, Turkestan; and Carloforte, Italy. The station in Charjui closed due to economic problems caused by war, but a new station opened in Kitab, Uzbekistan after World War I. Each observatory engaged in a program of observing the positions of 144 selected reference stars, and the data from each station were cross referenced to provide accurate measurements of the location of the North Pole.

International Latitude Service station in Ukiah, California. (Public domain image from Wikimedia Commons.)

In 1962, the International Time Bureau founded the International Polar Motion Service, which incorporated the International Latitude Service observations and additional astronomical observations to provide a reference of higher accuracy, suitable for both navigation and defining time relative to Earth’s rotation. Finally in 1987, the the International Astronomical Union and the International Union of Geodesy and Geophysics established the International Earth Rotation Service (IERS), which took over from the International Polar Motion Service. The IERS is the current authority responsible for timekeeping and Earth-based coordinate systems, including the definitions of time units, the introduction of leap seconds to keep clocks in synch with the Earth’s rotation, and definitions of latitude and longitude, as well as measurements of the motion of the Earth’s poles, which are necessary for accurate use of navigation systems such as GPS and Galileo.

The motion of Earth’s poles can be broken down into three components:

1. An annual elliptical wobble. Over the period of a year, the Earth’s poles move around in an ellipse, with the long axis of the ellipse about 6 metres in length. In March, the North Pole is about 6 metres from where it is in September (though see below). This motion is generally agreed by scientists to be caused by the annual shift in air pressure between winter and summer over the northern and southern hemispheres. In particular there is an imbalance between the Northern Atlantic ocean and Asia, with higher air pressure over the ocean in the northern winter, but higher air pressure over the Asian continent in summer. This change in the mass distribution of the atmosphere is enough to cause the observed wobble.

Annual wobble of North Pole

Annual elliptical wobble of the Earth’s North Pole. Deviation is given in milliarcseconds of axial tilt; 100 milliarcseconds corresponds to a bit over 3 metres at ground level. (Figure adapted from [1].)

2. Superimposed on the annual elliptical wobble is another, circular, wobble, with a period of around 433 days. This is called the Chandler wobble, named after its discoverer, American astronomer Seth Carlo Chandler, who found it in 1891. The Chandler wobble occurs because the Earth is not a perfect sphere. The Earth is slightly elliptical, with the radius at the equator about 20 kilometres larger than the polar radius. When elliptical objects spin, they experience a slight wobble in the rotation known as free nutation. This is the sort of wobble seen in a spinning rugby ball or American football in flight (where the effect is exaggerated by the ball’s exaggerated elliptical shape). This wobble would die away over time, but is driven by changes in the mass distribution of cold and warm water in the oceans and high and low pressure systems in the atmosphere. The Chandler wobble has a diameter of about 9 metres at the poles.

The combined effect of the annual wobble and the Chandler wobble is that the North and South Poles move in a spiralling pattern, sometimes circling with a diameter up to 15 metres, then reducing down to about 3 metres, before increasing again. This beat pattern occurs over a period of about 7 years.

Graph showing the movement of the North Pole over a period of 4500 days (12.3 years), with time on the vertical axis and the spiralling motion mapped in the x and y axes. The motion tickmarks are 0.1 arcsecond in rotation angle of the axis apart, corresponding to about 3 metres of motion along the ground at the Pole. (Public domain image from Wikimedia Commons.)

3. The third and final motion of the Earth’s poles is a systematic drift, of about 200 millimetres per year. Since 1900, the central point of the spiral wobbles of the North Pole has drifted by about 20 metres. This drift is caused by changes in the mass distribution of Earth due to shifts in its structure: movement of molten rock in the mantle, isostatic rebound of crust following the last glacial period, and more recently the melting of the Greenland ice sheet. The melting of the Greenland ice sheet in the last few decades has shifted the direction of polar drift dramatically; one of the serious indications of secondary changes to the Earth caused by human-induced climate change. Changes in Earth’s mass distribution alter its rotational moment of inertia, and the rotational axis adjusts to conserve angular momentum.

Motion of North Pole since 1900

Plot of motion of the North Pole since 1900. The actual position of the Pole from 2008 to 2014 is shown with blue crosses, showing the annual and Chandler wobbles. The mean position (i.e. the centre of the wobbles) is shown for 1900 to 2014 as the green line. The pole has mostly drifted towards the 80° west meridian, but has changed direction dramatically since 2000. (Figure reproduced from [2].)

Each of the three components of Earth’s polar motion are: (a) observable with 19th century technology, (b) accurately measurable using current technology, and (c) understandable and quantitatively explainable using the fact that the Earth is a rotating spheroid and our knowledge of its structure.

If the Earth were flat, it would not be possible to reconcile the changes in position of the North and South Poles with the known shifts in mass distribution of the Earth. The Chandler wobble would not even have any reason to exist at close to its observed period unless the Earth was an almost spherical ellipsoid.

References:

[1] Höpfner, J. “Polar motion at seasonal frequencies”. Journal of Geodynamics, 22, p. 51-61, 1996. https://doi.org/10.1016/0264-3707(96)00012-9

[2] Dick, W., Thaller, D. IERS Annual Report 2013. International Earth Rotation Service, 2014. https://www.iers.org/IERS/EN/Publications/AnnualReports/AnnualReport2013.html

13. Hydrostatic equilibrium

The theory of gravity is wildly successful in explaining and predicting the behaviours of masses. Isaac Newton’s formulation of gravity (published in his Principia Mathematica in 1686) is a simple formula that works very well for most circumstances of interest to people. When the gravitational potential energy or the velocity of a mass is very large, Albert Einstein’s general relativity (published 1915) is required to correctly determine behaviour. Newton’s gravity is in fact an approximation of general relativity that gives almost exactly the correct answer when the gravitational energy per unit mass is small compared to the speed of light squared, and the velocity is much smaller than the speed of light. For almost all calculation purposes, Newton’s law is sufficiently accurate to be used without worrying about the difference.

Newton’s law says that the force of gravitational attraction F between two bodies equals the universal gravitational constant G, multiplied by the masses of the two bodies m₁ and m₂, divided by the square of the distance r between them: F = G m₁ m₂/(r²).

Newton's law of gravitation

Newton’s law of gravitation describes the force F between two bodies m₁ and m₂ separated by a distance r between their centres of mass.

Newton himself had no idea why this simple formula worked. Although he showed that it was accurate to the limits of the measurements available to him, he was deeply concerned about its philosophical implications. In particular, he couldn’t imagine how such a force could occur between two bodies separated by any appreciable distance or the vacuum of space. He wrote in a letter to Richard Bentley in 1692:

“That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it.”

Newton was so concerned about this that he added an appendix to the second edition of the Principia – an essay titled the General Scholium. In this he wrote about the distinction between observational, experimental science, and the interpretation of observations (translated from the original Latin):

“I have not as yet been able to discover the reason for these properties of gravity from phenomena, and I do not feign hypotheses. For whatever is not deduced from the phenomena must be called a hypothesis; and hypotheses, whether metaphysical or physical, or based on occult qualities, or mechanical, have no place in experimental philosophy.”

In other words, Newton was being led by his observations to deduce physical laws and how the universe behaves. He refused to countenance speculation unsupported by evidence, and he accepted that the world behaved as observed, even if he didn’t like it. Commenting on Newton’s words in 1840, the philosopher William Whewell wrote:

“What is requisite is, that the hypotheses should be close to the facts, and not connected with them by other arbitrary and untried facts; and that the philosopher should be ready to resign it as soon as the facts refuse to confirm it.”

This affirms the position of a scientist as one who observes nature and tries to describe it as it is. Any hypothesis formed about how things are or why they behave the way they do must conform to all the known facts, and if any future observation contradicts the hypothesis, then the hypothesis must be abandoned (perhaps to be replaced with a different hypothesis). This is the scientific method in a nutshell, and guides our understanding of the shape of the Earth in these pages.

The universal gravitational constant G is a rather small number in familiar units: 6.674×10⁻¹¹ m³ kg⁻¹ s⁻². This means that the force of gravity between two everyday objects is so small as to be unnoticeable. For example, even large objects such as two 1-tonne cars a metre apart experience a gravitational force between them of only 6.674×10⁻⁵ newtons – far too small to move the cars against rolling friction, even with the brakes off. Also, the distance between the masses in Newton’s formula is the distance between the centres of mass of the objects, not the closest surfaces. The centres of mass of two cars can’t be brought closer together than about 2 metres in practice, even with the cars touching each other (unless you crush the cars).

Gravity really only starts to significantly affect things when you gather millions of tonnes of mass together. On Earth, the mass of the Earth (5.9722×10²⁴ kilograms) itself dominates our experience with gravity. Removing mass 2 from Newton’s formula, we can calculate the acceleration a towards the centre of mass of the Earth, caused by the Earth’s gravity, as experienced at the surface of the planet (r = 6370 kilometres): a = G m₁/(r²) = 6.674×10−11 × 5.9722×1024 / (6370×103)² = 9.82 m/s². This number matches experimental observations we can make of the gravity on the surface of the Earth (for example, using a pendulum: see also Airy’s coal pit experiment).

So large object like planets or other astronomical bodies experience a significant gravitational force on parts of themselves. Think about a tall mountain, such as Mount Everest. Let’s estimate the mass of Mount Everest – just roughly will do for our purposes. It is 8848 metres tall, above sea level. Let’s imagine it’s roughly a cone, with sides sloping at 45°. That makes the radius of the base 8848 metres, and its volume is π × 8848³ / 3 = 7.25×10¹¹ cubic metres. The density of granite is 2.75 tonnes per cubic metre, so the mass of Mount Everest is roughly 2×10¹⁵ kg. It experiences a gravitational force of approximately 2×10¹⁶ newtons, pulling it down towards the rest of the Earth.

Newton's law of gravitation

Approximating Mount Everest as a cone of rock to calculate the pressure on the base.

Obviously Mount Everest is strong enough to withstand this enormous force without collapsing. But how much higher could a mountain be without collapsing under its own mass? The taller a mountain gets, the more force pulls it down, but the structural strength of the rock making up the mountain does not increase. At some point there is a limit. Our conical Mount Everest model spreads that mass over an area of π × 8848² square metres. This means the pressure of the rock above on this area is 2×10¹⁶ / (π × 8848²) = 8×10⁷ pascals, or 80 megapascals (Mpa). Now, the compressive strength of granite is about 200 MPa. We’re pretty close already! Not to mention that rock can also shear and deform plastically, so we probably don’t even need to get as high as 200 MPa before something bad (or spectacular, depending on your point of view!) happens. A mountain twice as high as Everest would almost certainly be unstable and collapse very quickly.

As mountains get pushed up by tectonic activity, their bases spread out under the pressure of the rock above, so that they can’t exceed the limit of the tallest possible mountain. In practice, it turns out that glaciation also has a significant effect on the maximum height of mountains on Earth, limiting them to something not much higher than Everest [1].

Now, compared to the size of the Earth, even a mountain as tall as Everest is pretty insignificant. It is barely a thousandth of the radius of the planet. It’s often said that if shrunk down to the same size, the Earth would be smoother than a billiard ball. In a sense, this is actually true! Billiard and snooker balls are specified to be 52.5 mm in diameter, with a tolerance of 0.05 mm [2]. That is just under a 500th of the radius, so it would be acceptable to have billiard balls for professional play that are twice as rough as the Earth – although in practice I suspect that billiard balls are manufactured smoother than the quoted tolerance.

So, there is a physical limit to the strength of rock that means that Earth can’t have any protruding lumps of any significant size compared to its radius. Similarly, any deep trenches can’t be too deep either, or else they’ll collapse and fill in due to the gravitational stress on the rock pulling it together. The Earth is spherical in shape (more or less) because of the inevitable interaction of gravity and the structural strength of rock. Any astronomical body above a certain size will also necessarily be close to spherical in shape. The size may vary depending on the materials making up the body: rock is stronger than ice, so icy worlds will necessarily be spherical at smaller sizes than rocky ones.

The phenomenon of large bodies assuming a spherical shape is known as hydrostatic equilibrium, referring to the fact that this is the shape assumed by any body with no resistance to shear forces, in other words fluids. For ice and rock, the resistance to shear force is overcome by gravity for objects of size a few hundred to a thousand or so kilometres in diameter. The asteroid Ceres is a hydrostatic spherical shape, with a diameter of 945 km. On the other hand, Saturn’s moon Iapetus is the largest known object to deviate significantly from hydrostatic equilibrium, with a diameter of 1470 km. Iapetus is almost spherical, but has an unusual ridge of mountains running around its equator, with a height around 20 km – about 1/36 of the moon’s radius.

Iapetus, one of the moons of Saturn, photographed by NASA’s Cassini space probe. (Public domain image by NASA.)

It’s safe to say, however, that any planetary sized object has to be very close to spherical – or spheroidal if rotating rapidly, causing a slight bulge around the equator due to centrifugal force. This is because of Newton’s law of gravity, and the structural strength of rock. Our Earth, naturally, is such a sphere.

Flat Earth models must either conveniently ignore this conclusion of physics, or posit some otherwise unknown force that maintains the mass of the Earth in a flat, non-spherical shape. By doing so, they violate Newton’s principle that one must be guided by observation, and discard any hypothesis that does not fit the observed facts.

References:

[1] Mitchell, S. G., Humphries, E. E., “Glacial cirques and the relationship between equilibrium line altitudes and mountain range height”. Geology, 43, p. 35-38, 2015. https://doi.org/10.1130/G36180.1

[2] Archived from worldsnooker.com on archive.org: https://web.archive.org/web/20080801105033/http://www.worldsnooker.com/equipment.htm

11. Auroral ovals

Aurorae are visible light phenomena observed in the night sky, mostly at high latitudes corresponding to Arctic and Antarctic regions. An aurora can appear as an indistinct glow from a distance or as distinct shifting curtain-like formations of light, in various colours, when seen from nearby.

An aurora, observed near Eielson Air Force Base, near Fairbanks, Alaska. (Public domain image by Senior Airman Joshua Strang, United States Air Force.)

Aurorae are caused by the impact on Earth’s atmosphere of charged particles streaming from the sun, known as the solar wind.

Schematic representation of the solar wind streaming from the sun and interacting with the Earth’s magnetic field. The dashed lines indicate paths of solar particles towards Earth. The solid blue lines show Earth’s magnetic field. (Public domain image by NASA.)

The Earth’s magnetic field captures the particles and deflects them (according to the well-known laws of electromagnetism) so that they spiral downwards around magnetic field lines. The result is that the particles hit the atmosphere near the Earth’s magnetic poles.

Diagram of the solar wind interacting with Earth’s magnetic field (field lines in red). The magnetic field deflects the incoming particles around the Earth, except for a fraction of the particles that enter the magnetic polar funnels and spiral down towards Earth’s magnetic poles. (Public domain image by NASA. modified.)

The incoming high energy particles ionise nitrogen atoms in the upper atmosphere, as well as exciting oxygen atoms and nitrogen molecules into high energy states. The recombination of nitrogen and the relaxation of the high energy states results in the emission of photons. The light is produced between about 90 km and 150 km above the surface of the Earth, as shown by triangulating the positions of aurorae from multiple observing locations.

Observations of aurorae have established that they occur in nearly-circular elliptical rings of width equivalent to a few degrees of latitude (i.e. a few hundred kilometres), usually between 10° and 20° from the Earth’s magnetic poles. These rings, in the northern and southern hemispheres, are called the auroral ovals.

Northern auroral oval

Northern auroral oval observed on 22 January 2004. Figure reproduced from [1].

The auroral ovals are not precisely centred on the magnetic poles, but rather are pushed a few degrees towards the Earth’s night side. This is caused by the diurnal deflection of the Earth’s magnetic field by pressure from the charged particles of the solar wind.

Northern auroral oval observed in 1983 by Dynamics Explorer 1 satellite. The large bright patch at left is the daylight side of Earth. (Public domain image by NASA.)

The auroral ovals also expand when solar activity increases, particularly during solar storms, when increased particle emission from the sun and the resulting stronger solar wind compresses the Earth’s magnetic field, forcing field lines to move away from the poles.

But despite these variations, the auroral ovals in the northern and southern hemispheres move and change sizes more or less in unison, and are always of similar size.

Southern auroral oval observed in 2005 by IMAGE satellite, overlaid on a Blue Marble image of Earth. (Public domain image by NASA.)

You can see the current locations and sizes of both the northern and southern auroral ovals as forecast based on the solar wind and interplanetary magnetic field conditions as measured by the Deep Space Climate Observatory satellite at https://www.spaceweatherlive.com/en/auroral-activity/auroral-oval.

Current northern and southern auroral ovals as forecast by spaceweatherlive.com on 21 April, 2019. The auroral ovals are the same size and shape.

Earth is not the only planet to display aurorae. Jupiter has a strong magnetic field, which acts to funnel the solar wind towards its polar regions in the same way as Earth’s field does on Earth. Jupiter we can establish by simple observation from ground-based telescopes is close to spherical in shape and not a flat disc. Auroral ovals are observed on Jupiter around both the northern and southern magnetic poles, exactly analogously to on Earth: of close to the same size and shape.

Northern auroral ovals on Jupiter

Auroral ovals on Jupiter observed in the northern and southern polar regions by the Hubble Space Telescope, using the Wide Field Planetary Camera (1996) and the Space Telescope Imaging Spectrograph (1997-2001). Figure reproduced from [2].

Similar auroral ovals are also seen on Saturn, in both the northern and southern hemispheres [3][4]. And just for the record, Saturn is also easily shown to be spherical in shape, and not a flat disc.

Now, we have established that auroral ovals appear on three different planets, with the southern and northern ovals of close to the same sizes and shapes on each individual planet. Everything is consistent and readily understandable – as long as you assume that the Earth is spherical like Jupiter and Saturn.

If the Earth is flat, however, then the distributions of aurorae in the north and south map to very different shapes and sizes – with no ready explanation for either the shapes or their differences. In particular, large parts of the southern auroral oval end up being extremely far from the southern magnetic pole, in defiance of the electromagnetic mechanism that causes aurorae in the first place.

Auroral ovals on a flat Earth

Auroral ovals in their observed locations, mapped onto a flat disc Earth. The ovals are vastly different sizes.

So the positions of aurorae on a flat Earth cannot be readily explained by known laws of physics, and they also do not resemble the locations and sizes of auroral ovals as observed on other planets. All of these problems go away and become self-consistent if the Earth is a globe.

References:

[1] Safargaleev, V., Sergienko, T., Nilsson, H., Kozlovsky, A., Massetti, S., Osipenko1, S., Kotikov, A. “Combined optical, EISCAT and magnetic observations of the omega bands/Ps6 pulsations and an auroral torch in the late morning hours: a case study”. Annales Geophysicae, 23, p. 1821-1838, 2005. https://doi.org/10.5194/angeo-23-1821-2005

[2] Grodent, D.,Clarke, J. T., Kim, J., Waite Jr., J. H., Cowley, S. W. H. “Jupiter’s main auroral oval observed with HST‐STIS”. Journal of Geophysical Research, 108, p. 1389-1404, 2003. https://doi.org/10.1029/2003JA009921

[3] Cowley, S. W. H., Bunce, E. J., Prangé, R. “Saturn’s polar ionospheric flows and their relation to the main auroral oval”. Annales Geophysicae, 22, p.1379-1394, 2004. https://doi.org/10.5194/angeo-22-1379-2004

[4] Nichols, J. D., Clarke, J. T., Cowley, S. W. H., Duval, J., Farmer, A. J., Gérard, J.‐C., Grodent, D., Wannawichian, S. “Oscillation of Saturn’s southern auroral oval”. Journal of Geophysical Research, 113, A11205, 2008. https://doi.org/10.1029/2008JA013444

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: