[audio version of this article]
Determining that the Earth is not flat is not a feat that requires space age technology to achieve. In fact, you can demonstrate it with not much more than a stick and some elementary geometry. And this was indeed done in antiquity.
Around the year 240 BC the Greek scholar Eratosthenes realised the significance of certain observations based on shadows cast by the sun. Not only did he show that the Earth is not flat, he did an experiment to measure the circumference of the spherical Earth.
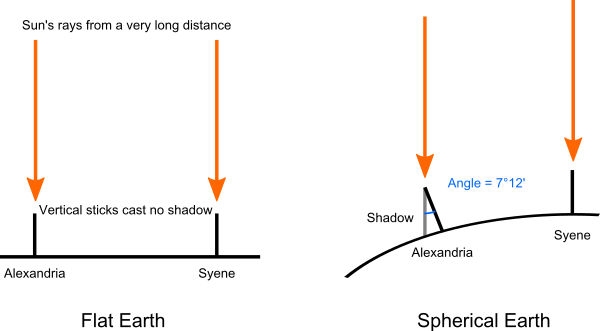
Eratosthenes was the head librarian at the great Library of Alexandria. He had heard that at noon on the day of the summer solstice, the sun shone directly down a vertical well in the Egyptian city of Syene, where the modern city of Aswan now stands. Equivalently, at noon on the solstice, a stick placed vertically in the ground would cast no shadow, because the sun was directly overhead. This property was well known amongst geographers as a curiosity, because it didn’t happen at any cities further north.
Eratosthenes took it a step further by thinking about why this was the case. He figured that the sun was a very long way away, at least much further away than, say, the distance between Syene and Alexandria on the northern coast of Egypt – measured by surveyors to be 5000 stadia. (According to the writings of Eusebius of Caesarea, Eratosthenes in fact calculated the distance from the Earth to the sun, possibly using a method developed by Aristarchus. Eusebius’s figures are ambiguous, but can be interpreted as giving a figure of 149 million km, almost exactly correct.) If the Earth were flat, the sun would be directly overhead everywhere at the same time. But this was not the case. At noon on the summer solstice, a vertical stick in Alexandria cast a definite shadow. He realised not only that the Earth’s surface must be curved, but that he could use the length of the shadow to calculate how big the Earth was.
By measuring the length of a vertical stick and its shadow in Alexandria at noon on the solstice, Eratosthenes calculated that the sun was at an elevation of 7°12′ to the vertical. The angle of 7°12′ is exactly one fiftieth of a circle. Eratosthenes also figured that Alexandria was pretty much due north of Syene. So this meant that the distance from Syene to Alexandria must be one fiftieth of the circumference of the Earth. So the circumference of the Earth, Eratosthenes concluded, must be 250,000 stadia.
How long is a classical Greek/Egyptian stadion? There is some debate over this. Some scholars suggest that Egyptian surveyors used a stadion of 174.6 metres, giving a circumference of 43,650 km. Others think they used a stadion of 184.8 m, giving a result of 46,000 km. Modern measurements of the Earth’s circumference around the poles set the figure at 40,008 km. So depending which figure we use for the stadion, Eratosthenes got the answer right to within 9% or 15%, respectively. Not too bad for a measurement made with nothing but a stick!
The main mistake Eratosthenes made was assuming Alexandria was due north of Syene. The distance needs to be adjusted to remove the east-west offset, and if you do this you get an answer even closer to the modern measurement. The rest of the error is likely mostly due to imprecision in measuring distances and angles. We might even speculate that Eratosthenes did a bit of rounding to make his measured angle exactly one fiftieth of a circle.
Can we do better than Eratosthenes? With your help, I’d like to do an experiment and collect some data, and see how accurately we get to measuring the circumference of the Earth. Rather than use the northern summer solstice, we’re going to use the March equinox, which conveniently happens less than two weeks from when I post this entry: on 20 March (or 21 March in some time zones). On that date, I’d like you to help me by doing a simple measurement, wherever you happen to be. Full instructions follow:
- Work out the date closest to the equinox where you are. For time zones of UTC+2 or less (including all of the Americas, Europe, and most of Africa) it’s on 20 March, 2019. For time zones UTC+3 or more (including Eastern Africa, Asia, Australia) it’s on 21 March. Actually if you’re in Europe or Africa, the equinox is close to midnight this year, so it probably doesn’t matter much if you do this on 20 or 21 March.
- Work out what time is local solar noon where you are. (This is the time when the sun is directly over the meridian of longitude running through your location, and it’s usually not exactly at 12:00.) For this, use TimeandDate.com’s Sun Calculator. Enter your location in the search box. When the page brings up the data for your location, scroll down to the calendar table and find the entry for the date you have worked out at step 1. Look at the column marked “Solar noon” and read the time given there. You now have the date and the exact time when you need to make your measurement. Hopefully it will be sunny for you then!
- Work out where you’ll be at that time on that date. Find a nice flat, level area there. Get a straight stick – the longer the more accurate. Measure the length of the stick.
- On the equinox date, at the exact time of your local solar noon: If it’s sunny, place your stick vertically on your flat area. Do this as accurately as you can – use a spirit level or inclinometer if you can. If you don’t have one, let the stick dangle from the top, with the bottom just barely touching the ground. With the stick vertical, measure the length of its shadow cast by the sun, again as accurately as you can manage. Using a friend to help you will make things easier. If it’s not sunny at the right time, oh well, I appreciate your help anyway, but that’s how science works sometimes!
- Once you have the shadow length, you’re ready to report your data! I need to know: (1) Where you were – city, state, country – enough that I don’t get it wrong. If you can tell me your exact latitude (using Google maps or a GPS), even better. (2) The length of your vertical stick. (3) The length of the shadow you measured. Send these three bits of data to me by email [dmm at dangermouse.net], by the end of March.
I’ll calculate the results, do some statistics, and come up with our very own measurement of the circumference of the Earth! I’ll post the results here in April.

I have this in my calendar, David, although I do have the supernatural ability to bring on cloud cover when I’m trying to observe celestial phenomena 🙂
Not sure what tool you are using to do your blog, but it would be nice if it had a way to share a post on modern social media outlets, seems a bit old fashioned that it does not. It would help to distribute your request for data and other interesting posts.
Good idea! I’ve added some sharing buttons.
Shared your blog post – [https://www.facebook.com/ilskinner/posts/2582063738473825].
I like this experiment, although it’s a little unsatisfying to have to look up some data on a website; I mean, the website is probably in the thrall of the round-earth conspiracy and might be lying to me. It would be better to measure for myself when solar noon is; it is when the direction of the shadow is perfectly north or south (it will list to the west before that and to the east after), so I just to measure this a few times before and after when I suspect solar noon will be to be sure. (If I’m worried that I can’t trust my directions, then I can measure the lengths at various times as well, and the noon length will stand out in the middle; I can’t tell in my head whether it will be longest or the shortest, but it should be clear either way.) However, I realize that this would cut down on participation a lot, so I don’t blame you for leaving it out.
This is a great idea! Going to get my physics class prepped to participate, then hope for good weather!
Is this experiment to show that you can calculate latitudes from measuring the lengths of sticks and the shadows they cast at local solar noon on the equinox? You can’t get from here to calculating the circumference of the Earth unless you, like Eratosthenes, already know the distance (and direction) between some of the points of measurement. Calculating the distances from the latitudes and longitudes is cheating. Even though you are working on spheres here, you should try to avoid circular reasoning.
In principle we can measure the distances and directions by doing a geodetic survey. In practice, that’s too difficult for this relatively simple crowdsourced experiment, so yes, I’m taking a bit of a shortcut. The aim is not to actually do it entirely from first principles, but to have a bit of fun, show that in principle we could if we really took the effort, and to see how accurate we can get the final number.
Curious: Would this experiment yield the same results if the earth were flat and the sun’s distance above the well in Cairo was exactly the radius measurement of the spherical earth? Assuming we did not have the figure provided by Aristarchus of Samos. In fact, an an aside describing Aristarchus’ method might be a nice addition to support the assumption.
I haven’t done the geometry in detail, but you can have the shadows in Syene and Alexandria behave this way with a flat Earth and a much closer sun, yes. However the variation of shadow lengths as you move further north or south will be different, so you can differentiate that way. It’ll be a sine curve on a spherical Earth, but something else on a flat one.
The aside is a good idea.
Sorry David, trying to help here in the UK but it is heavily overcast where I am. I hope tomorrow will be better since being in UTC+0 it shouldn’t make much difference which day I take a measurement (although being the UK the chance of sun is slim at best at this time of year).
Great and interesting series of articles, will you cover the Bedford Level experiment?
Yes, the Bedford Level is on my list. Thanks for trying, and I hope the weather is fairer tomorrow!
Measurements take and sent. Hope you get what you’re looking for!
Done! There was enough cloud cover at the time to make the shadow a little fuzzy, but the error was probably less than 1%
Can you talk a bit about the assumption that the sun is really far away? I’ve pulled this experiment out when talking with a flat-earther, and his first counter was that the sun is much closer so the angles of light are going to be different. I’m assuming that parallax would be involved, but did Eratosthenes measure this, or was it just a common assumption at the time?
I just came across this site, wondering if anyone performed this experiment in a modern way. After reading the measurement criteria, I think you also need to take height above sea level into account in order to narrow down the diversity in measurements.
Hi,
Today is: 10 Sept/2024.
If you wish, I can still do the stick and angle measurement on 21/22 Sept.
Let me know if you are still interested in the experiment.
Thanks a lot for the detailed article.