[audio version of this article]
Gravity is the force that causes objects to fall towards the ground. Observations of the movements of the planets led Isaac Newton in 1687 to publish his formulation of the force between two objects caused by gravity, stating that the force is proportional to the masses of the objects and the reciprocal of the square of the distance between them. This simple relationship has been wildly successful, although it was superseded in 1915 when Albert Einstein published his general theory of relativity. Einstein’s model differs from Newton’s only by imperceptible amounts, except when extremely large masses or speeds close to the speed of light are involved. For something the size of Earth, Newton’s law of gravity works just fine.
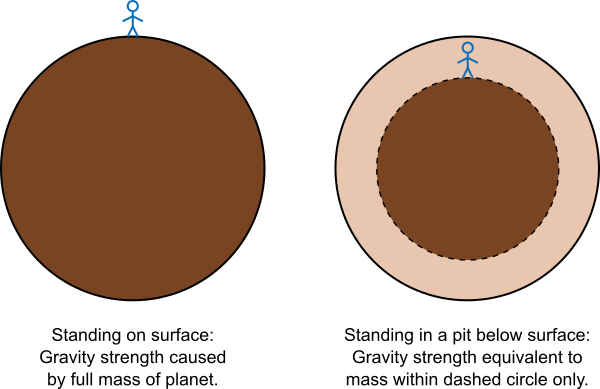
Given Newton’s law, some relatively straightforward vector calculus can be used to prove Gauss’s law for gravity, which gives a relationship between the gravitational flux of an enclosed surface and the amount of mass inside that surface. For symmetrical cases like spherical objects, the gravitational flux is just the gravitational field strength multiplied by the surface area of the sphere. The details are not as important here as the result: For a spherical object, the gravitational force of the object at any point—outside or inside the object—depends only on the distance from the centre of the object and the amount of mass within a sphere of that radius.
So consider the Earth – assuming it’s spherical. If you are on the surface or above it, the gravitational force you feel is produced by the entire mass of the Earth. However, if you are beneath the surface of the Earth, all of the mass of the Earth at shallower depths has no effect on you – the gravitational pull in all different directions cancels exactly to zero. You only feel the gravity from the part of the Earth that is deeper than you are. This means that as you burrow deeper into the Earth, the gravitational force you feel decreases, until eventually, if it were possible to reach the centre of the Earth, it would be zero. On the other hand, if the Earth is flat there’s no a priori reason to think that gravity should get progressively less strong as you go deeper underground.
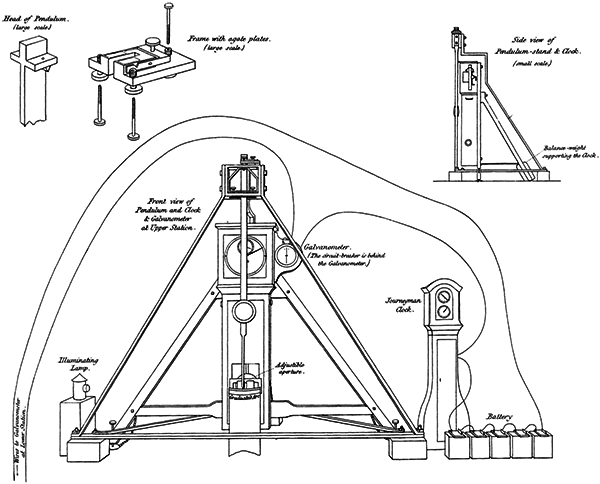
Gravitational force, it turns out, is fairly easy to measure. The period of a swinging pendulum depends on the force of gravity, and we’ve been able to measure small changes in the period of a pendulum fairly precisely for hundreds of years. Since before Newton’s time, in fact. The Elizabethan-era philosopher Francis Bacon first suggested taking pendulums up mountains to see if gravity varied with altitude in 1620. This experiment was actually carried out in 1737 by the French mathematician Pierre Bouguer, in the Peruvian Andes. (And perhaps more about that particular experiment another day.)
But in the 1820s the British astronomer George Biddell Airy realised that if you measured the force of gravity at the surface of the Earth, and also down a deep mine, you should get two different values. Not only that, but the size of the difference and the depth of the mine could be used to calculate the density of the Earth. He began experimenting in 1826, but unfortunately his first attempt failed due to a mine flood. Airy was a busy guy, accepting the post of Astronomer Royal in 1835 and discovering and inventing a whole bunch of other stuff. But finally in 1856 he tried the gravity experiment again.
Airy used a coal pit at the Harton Colliery, near Harton in the county of Tyne and Wear in north-eastern England. The pit was 1260 feet (384 metres) deep, and at the bottom Airy built a sophisticated pendulum and time measurement system. He compared timing measurements made at the surface and the bottom of the pit over a period of 60 hours with the same length pendulum, and discovered that the pendulum at the bottom of the pit ran slower by 2.24 seconds per day.
For our purposes, this difference is the evidence we need that the Earth is spherical. We predicted that if the Earth is spherical then gravity should be lower at the bottom of a pit than on the surface, and Airy showed that is indeed true. But he didn’t stop there, because of course he already knew that the Earth was round, and its circumference. With that piece of data and his pendulum measurement, he could calculate the density of the Earth, finding a figure of 6.62 times the density of water.
As it turns out, modern measurements give a density of 5.51, about 17% less. Airy’s coal pit experiment was very fiddly, and it’s a credit that he got so close to the correct answer.
Now remember that previously we’ve shown that Eratosthenes measured the size of the Earth, simply using sticks and shadows. Airy’s experiment shows that once you know the size of Earth, you can get a decent measurement of the density of the planet using something as simple as a pendulum. And once you know the size and the density of something, its mass is simply the volume multiplied by the density.
In other words, if you’re clever enough you can measure the mass of the Earth with a stick, a length of string, and a weight.
References:
[1] Airy, G. B., “Lecture on the Pendulum-Experiments at Harton Pit”, lecture delivered at Central Hall, South Shields, 24 October 1854, Longman & Co., London. https://books.google.com/books?id=JRZcAAAAQAAJ
[2] Airy, G. B., “Account of Pendulum Experiments Undertaken in the Harton Colliery, for the Purpose of Determining the Mean Density of the Earth”, Philosophical Transactions of the Royal Society of London, 146, p. 297-355, 1856. https://doi.org/10.1098/rstl.1856.0015


That’s very cool. I actually know all the math involved–the calculation is used as an example in calculus class, after all. I never actually thought about doing the experiment with a pendulum in a mine, though. Thanks!
This was a question at my interview to do physics at Newcastle university, also in Tyne and Wear!
You are wrong on the bit about “if the Earth is flat there’s no a priori reason to think that gravity should get progressively less strong as you go deeper underground”. If you move 300 metres underground, the mass above you would pull up, with only the part beneath you pulling down. There wouldn’t be the neat “it all cancels out” effect you see with a perfect sphere. Instead, the measurable force would drop off faster – if 1% of the Earth’s mass is “above” you in a spherical model you would see a 1% drop in measurable gravity, in a flat model you’d see 2%. So you can still distinguish the two models, making some fairly bold assumptions about the mass of the Earth and relative density.
You should also be able to use this to measure the thickness of the flat earth…
It depends on what assumptions you make about the Flat Earth. Many Flat Earth theorists believe that the apparent force pulling us down to the surface is caused by a uniform acceleration of the disc upwards through space. In this case, “gravity” should not change at all as you move up or down.
If you assume gravity on a Flat Earth follows Newton’s law, then yes, it should reduce in strength as you go underground. But it has much bigger problems than that (as we’ll see later on…)!
Problems like…wouldn’t the gravity to the sides be measurable in a Flat Earth theory? 😮
Which just proves that there’s no point in arguing with those who want to throw easily observable science out the window…
But, yes, this is the basic problem with “flat earth” – a plumb line and a bob shows how far you are from the centre of the “flat earth”. Worse, where’s the edge? Can we go and have a look?
Which is why no one serious has ever believed in a flat earth – it is far too easy to disprove.
Most flat earth ears don’t believe there is such a thing as gravity. They believe that the earth and all is accelerating trough space at
9.81 m/s^2. This provides the sensation of weight.
If this were true, this force would be the same everywhere on the surface of earth or under the earth as well. You’re taught in freshman analytical chemistry that spring balances don’t give the same mass and have to be calibrated based on latitude and elevation, to begin with. The web site bellow is admirable as far as measuring the force of gravity but way off in regards to the speed of gravity. That’s been shown to be the speed of light.
“…if you’re clever enough you can measure the mass of the Earth with a stick, a length of string, and a weight.”
That’s some Doctor Who shit right there!
The pendulum got him the relative densities of the surface layers (above the mine) and of the bulk of the Earth. Absolute density followed from estimates of the density of the surface, using direct measurements on rocks.
Ah, that does make more sense. They seem to have skimmed over that detail in the accounts I read.
“[…] stating that the force is proportional to the masses of the objects and the reciprocal of the distance between them.”
Shouldn’t it be “the reciprocal of the square of the distance between them”?
“[…] if you’re clever enough you can measure the mass of the Earth with a stick, a length of string, and a weight.”
You also need a way to measure time.
Besides, great article! As always.
I wasn’t aware of the Gauss’ law for gravity: I only “felt” it right at a semiconscious level but I never stopped to actually search for an answer.
Thank you.
Oops, I’ve fixed the typo, thanks. And to measure time all you need is a string and a weight… Well, I suppose you need a way to compare the time measurements at the top and bottom of the pit, so yes, that’s an additional requirement.
It should be enough to have a synchronization mechanism : for instance if a flash can be seen from both the surface and the bottom of the mine (considering that *c* is infinite for our purposes). Then count the number of beats of the pendulum at both sites between two such synchronization events.
“You only feel the gravity from the part of the Earth that is deeper than you are. This means that as you burrow deeper into the Earth, the gravitational force you feel decreases.”
That logic is flawed, unfortunately. As you burrow deeper into the Earth, you not only reduce the mass of “the part of the Earth that is deeper than you are”, but you are also reducing the distance that separates you from that mass. The reduced distance, unlike the reduced mass, works towards an *increase* of the gravitational force. The actual underground gravity is a combination of these two trends, and depends on the local density VS the average density of “the part of the Earth that is deeper than you are”.
IF you assume the Earth to be a homogeneous sphere (with a uniform density profile), then the “deeper-than-you-are” mass scales as the cube of the distance to the center, which, combined with the inverse distance squared of Newton’s law, gives you a linear decrease of the gravitational force all the way towards the center. But that’s a big IF!
The *actual* Earth has a massive core and a relatively lightweight mantle and crust, and the distribution of mass is in fact such that the gravitational force *increases* as you burrow underground, and stays close to 10m/s2 about halfway to Earth’s center. The naive “linear decrease” simply doesn’t exist except near the center of the core.
The good news is that Airy got everything right, of course. The result of his coal pit experiment is that the gravity at the bottom of the pit is *larger* than at the surface (by about 1/19286 of the surface amount). He then combined this increase rate with the known density of surface rocks to estimate the average density of the Earth as a whole.
But the bad news is that your article is misinterpreting Airy’s coal pit measurements (he confirmed that the gravitation force is *larger* underground than at the surface, whereas you are implying the opposite), and you are confused about his method for estimating the average density of the Earth (apart from the known radius of the Earth and the downwards *increase* rate of the gravity, he uses the known density of the surface rocks and a not-so-trivial differential formula). So, please fix the article ^_^