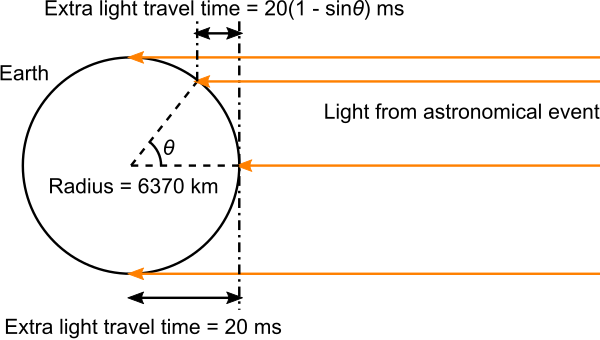
The Ancients had the technology and cleverness to work out the shape of the Earth and its diameter (see 2. Eratosthenes’ measurement). However, they had no reliable method to measure the mass of the Earth, or equivalently its density, which gives the mass once you know the volume. You could assume that the Earth has a density similar to rock throughout, but there was no way of knowing if that was correct.
In fact we had no measurement of the density or mass of the Earth until the 18th century. Perhaps surprisingly, there wasn’t even any observational evidence to decide whether the Earth was actually a solid object, or a hollow shell with a relatively thin solid crust. As late as 1692 the prominent scientist Edmond Halley proposed that the Earth might be composed of a spherical shell around 800 km thick, with two smaller shells inside it and a solid core, all separated by a “luminous” atmosphere (which could escape and cause the aurora borealis).

Structure of the Earth as proposed by Edmond Halley in 1692, with solid shells (brown) separated by a luminous atmosphere, shown in cross section.
In his 1687 publication of Philosophiæ Naturalis Principia Mathematica, Isaac Newton presented his theory of universal gravitation. Although this provided explicit equations relating the physical properties of gravitational force, mass, and size, for the cases of astronomical objects there were still more than one unknown value, so the equations could not be solved to determine the absolute masses or densities of planets. The best astronomers could do was determine ratios of densities of one planet to another.
But Newton not only proposed his formulation of gravity as a theoretical construct – he also suggested a possible experiment that could be done to test it. As observed by common experience, objects near the surface of the Earth fall downwards – they are attracted towards the centre of the Earth (more precisely, the Earth’s centre of mass). But if the attractive force of gravity is generated by mass as per Newton’s formulation, then unusual concentrations of mass should change the direction of the gravitational pull a little.
We’ve already seen in Proof 24. “Gravitational acceleration variation” that the strength of Earth’s gravitational pull varies across the Earth’s surface due to differences in altitude and density within the Earth. Now imagine a large concentration of mass on the surface of the Earth. If Newton is correct, then such a mass should pull things towards it. The attraction to the centre of the Earth is much stronger, so the direction of the overall gravitational pull should still be almost downwards, but there should be a slight deflection towards the large mass.
There are some convenient large masses on the surface of the Earth. We call them mountains. Newton conceived that one could go somewhere near a large mountain and measure the difference in angle between a plumb line (which indicates the direction of gravity, and is commonly called “vertical”) and a line pointing towards the Earth’s centre of mass (which does not have a well-defined name, since it is more difficult to measure and differs from a plumb line by an amount too small to be significant in engineering or construction – for the purposes of this proof only, I shall abbreviate it to “downwards”). However, Newton believed that any such difference would be too small to measure in practice. He writes in the Principia, Book 3: On the system of the world:
Hence a sphere of one foot in diameter, and of a like nature to the earth, would attract a small body placed near its surface with a force 20,000,000 times less than the earth would do if placed near its surface; but so small a force could produce no sensible effect. If two such spheres were distant but by 1/4 of an inch, they would not, even in spaces void of resistance, come together by the force of their mutual attraction in less than a month’s time; and lesser spheres will come together at a rate yet slower, namely in the proportion of their diameters. Nay, whole mountains will not be sufficient to produce any sensible effect. A mountain of an hemispherical figure, three miles high, and six broad, will not, by its attraction, draw the pendulum two minutes out of the true perpendicular; and it is only in the great bodies of the planets that these forces are to be perceived.[1]
Here is where Newton’s lack of experience as an experimentalist let him down. Two minutes of arc was already within the accuracies of stellar positions claimed by Tycho Brahe some 80 years earlier. If Newton had merely asked astronomers if they could measure a deflection of such a small size, they would likely have answered yes.

Engraving of Tycho Brahe observing in his observatory at Uraniborg, Sweden. (Public domain image from Wikimedia Commons.)
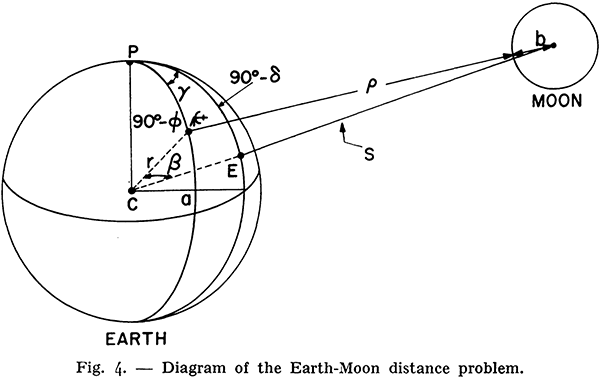
If you can measure how big the deflection angle is with sufficient accuracy, then you can use that measurement to calculate the density of the Earth in terms of the density of the mountain:
ρE/ρM = (VM/VE) (rE/d)2 / tan θ
where:
ρE is the density of the Earth,
ρM is the density of the mountain,
VE is the volume of the Earth,
VM is the volume of the mountain,
rE is the radius of the Earth,
d is the horizontal distance from the centre of the mountain to the plumb bob, and
θ is the angle of deflection of the plumb line from “downwards”.
The volume of the mountain can be estimated from its size and shape, and the density may be assumed to be that of common types of rock. All the other values were known, leaving the as yet unknown density of the Earth as a function of the deflection angle.
Two French astronomers, Pierre Bouguer (who we met in 4. Airy’s coal pit experiment) and Charles Marie de La Condamine, were the first to attempt to make the measurement. In 1735 they led an expedition to South America to measure the length of an arc of one degree of latitude along a line of longitude near the equator. This was part of an experiment by the French Academy of Sciences—along with simultaneous expedition to Lapland to make a similar measurement near the North Pole—to measure the shape of the Earth. Not whether it was spherical; any difference between the measurements would show if it was more accurately a prolate or an oblate ellipsoid.
Bouguer and La Condamine spent ten years on their expedition, making many other physical, geographical, biological, and ethnographical studies. One experiment they tried in 1738 was measuring the deflection of a plumb bob near the 6263 metre high volcano Chimborazo, in modern day Ecuador.

The volcano Chimborazo in Ecuador. (Creative Commons Attribution 2.0 image by David Ceballos, from Flickr.)
They climbed to an altitude of 4680 m on one flank of the mountain and 4340 m on the other side, battling harsh weather to take the two measurements. Taking two measurements on opposite sides of the mountain allows a subtraction to remove sources of error in locating the “downwards” direction, leaving behind the difference in angle between the two plumb bob directions, which is twice the desired deflection. Bouguer and La Condamine measured a deflection of 8 seconds of arc, however they considered the circumstances so difficult as to render it unreliable. But they did state that this measurement gave a large value for the Earth’s density, thus disproving the hypothesis that the Earth was hollow.
A more precise measurement of the gravitational deflection of a mountain had to wait until 1772, when Astronomer Royal Nevil Maskelyne made a proposal to repeat the experiment to the Royal Society of London.[2] The Society approved, and appointed the quaintly named Committee of Attraction to ponder the proposal. The committee (counting Joseph Banks and Benjamin Franklin among its members) despatched astronomer and surveyor Charles Mason (of Mason-Dixon line fame) to find a suitable mountain. He came back with Schiehallion, a 1083 m peak in central Scotland.

Schiehallion in central Scotland. (Creative Commons Attribution 3.0 Unported image by Wikipedia user Andrew2606, from Wikimedia Commons.)
Schiehallion had several advantages for the measurement. It’s conveniently located for a British expedition. It’s an isolated peak, with no other mountains nearby that could substantially complicate the effects of gravity in the region. It has a very symmetrical shape, making it easy to estimate the volume with some accuracy. And the northern and southern slopes are very steep, which means that by doing the experiment on those sides, the plumb bob can be positioned relatively close to the centre of mass of the mountain, increasing the deflection and making it easier to measure.
Maskelyne himself led the expedition, taking temporary leave from his post as Astronomer Royal. The party built temporary observatories on the northern and southern flanks of Schiehallion, from which they made frequent observations of overhead stars to determine the zenith line (marking the “downwards” direction), so they could compare it to the direction of the hanging plumb line. Maskelyne and his team spent 6 weeks at the southern observatory, followed by 10.5 weeks at the northern one, battling inclement weather to take the required number of observations.[3]
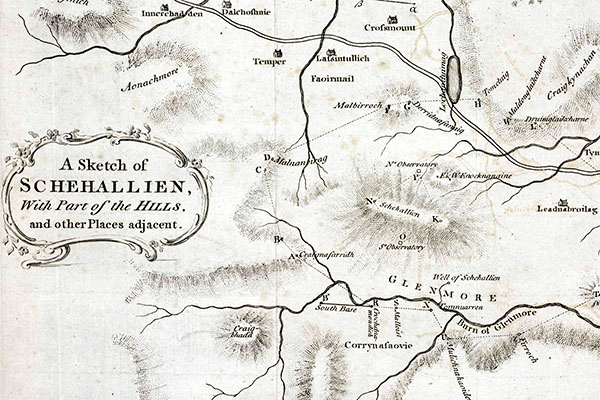
Map of Schiehallion and surrounds. The mountain forms a short ridge running approximately east-west. The positions of the north and south observatories can be seen. (Reproduced from [6].)
Maskelyne had calculated that if the Earth as a whole had the same density as the mountain (i.e. that of quartzite rock), then they should have observed a deflection of the plumb line relative to “downwards” of 20.9 seconds of arc. Preliminary calculations showed a deflection of about half that, meaning the Earth was roughly twice as dense as the mountain.
To mark the successful conclusion of the observations, the expedition celebrated with a rollicking good party. Plenty of alcohol was imbibed (quite possibly Scotch whisky). In the revelry, unfortunately someone accidentally set fire to the northern observatory and it burnt to the ground. The fire claimed the violin of one Duncan Robertson, a junior member of the expedition who had helped to pass the long cold nights of observation by entertaining the other members with his playing. Later, a grateful Maskelyne sent Robertson a replacement violin – not just any violin, but one made by the master craftsman Antonio Stradivari.[4][5]
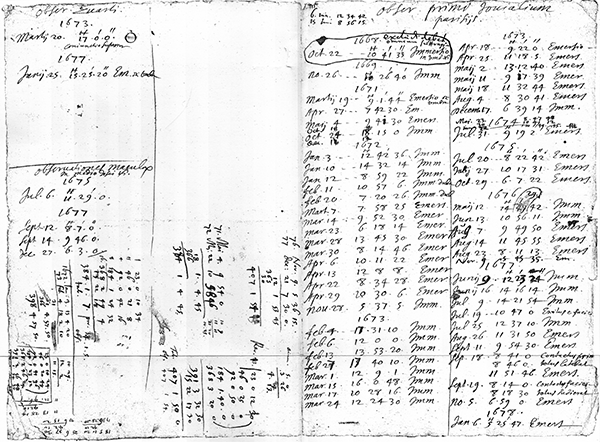
The mathematician and surveyor Charles Hutton was charged with doing the detailed calculations of the result. He published them in a mammoth 100-page paper in 1778.[6] His final conclusion was that the density of the Earth was 1.8 times the density of the quartzite in Schiehallion, or about 4.5 g/cm3. Since this was so much higher than the densities of various types of rock (typically between 2 and 3 g/cm3), Hutton concluded (correctly) that much of the core of the Earth must be metal, and he calculated that about 65% of the Earth’s diameter must be a metallic core (a little higher than current measurements of 55%).

Extract of Hutton’s paper, where he states that roughly 2/3 of the diameter of the Earth must be metallic to account for the measured density. This page also shows Hutton’s calculations of the densities of solar system bodies. (Reproduced from [6].)
This was the very first time that we had any estimate of the density/mass of the Earth, and Hutton also used it to calculate the densities of the Sun, the Moon, and the planets (out to Saturn) based on their known astronomical properties, mostly to within about 20% of the modern values. So the Schiehallion experiment was groundbreaking and significantly increased our fundamental understanding of the Earth and the solar system.
Later experiments confirmed the general nature of the result and refined the figures for the density and structure of the Earth. In particular, Henry Cavendish—a chemist who 20 years earlier had discovered the elemental nature of hydrogen and made several other discoveries about air and elemental gases—turned his attention to physics and performed what has become known as the Cavendish experiment in 1797-98. He constructed a finely balanced mechanism with which he could measure the tiny gravitational attractive force between two balls of lead, which allowed the measurement of the (then unknown) value of Newton’s gravitational constant. Knowing this value, it becomes possible to directly plug in values for the size of the Earth and the acceleration due to gravity and determine the mass of the Earth. Cavendish’s result was accurate to about 1%, confirming Hutton’s conclusion that the Earth must have a core denser than rock. And then in the 20th century, seismology allowed us to confirm the existence of discrete layers within the Earth, with the central core made primarily of metal (a story for a future Proof).

Drawing of Henry Cavendish. (Creative Commons Attribution 4.0 International image by the Wellcome Collection of the British Library, from Wikimedia Commons.)
Of course, the conclusions of the Schiehallion experiment—consistent with later experiments using independent methods—depend on the fact that the Earth is very close to spherical, and the fact that gravity works as Newton said (disregarding the later refinement by Einstein, which is not significant here). One of the more popular Flat Earth models assumes that gravity does not even exist as a force, and that objects “fall” to Earth because the Flat Earth is actually accelerating upwards. In such a model, objects always fall directly “downwards” and there is no deflection caused by large masses such as mountains. The Schiehallion experiment directly and simply disproves this Flat Earth model.
If we suppose that a Flat Earth somehow manages to exist with Newtonian gravity (in itself virtually impossible, see 13. Hydrostatic equilibrium), we could posit something like the 859 km thick flat disc mentioned in 34. Earth’s internal heat. Firstly, Newtonian gravity on such a disc would not always pull perpendicular to the ground – inhabitants near the circumference would be pulled at a substantial angle towards the centre of the disc. Ignoring this, if you managed to do the Schiehallion experiment (say at the North Pole), the distance rE in the equation would be effectively 430 km (the distance to the centre of mass of the disc) rather than the radius of the spherical Earth, 6378 km. This should make the observed deflection angle approximately (6378/430)2 = 220 times smaller! Then the observed deflections would imply that the density of the Earth is 220 times higher, or around 990 g/cm3, about 6 times as dense as the core of the Sun. Which is then inconsistent with the assumed density being the same as the spherical Earth (among other problems).
On the other hand, if we allow the density to be a free parameter, we can solve the gravitational and geometric equations simultaneously to derive the thickness of the Flat Earth disc in a “consistent” manner. This produces a thickness of 3020 km, and a density of 92 g/cm3. Which is over 4 times as dense as osmium, the densest substance at non-stellar pressures. So we’ve shown that the Schiehallion experiment proves that this “Newtonian Flat Earth” model cannot possibly be composed of any known material.
Basically, the observations of the Schiehallion experiment cannot be made consistent with a flat Earth, thus providing evidence that the Earth is a globe.
References:
[1] Newton, I. Philosophiae Naturalis Principia Mathematica (1687). Trans. Andrew Motte, 1729.
[2] Maskelyne, N. “A proposal for measuring the attraction of some hill in this Kingdom”. Philosophical Transactions of the Royal Society, 65, p. 495-499, 1772. https://doi.org/10.1098/rstl.1775.0049
[3]. Sillitto, R.M. “Maskelyne on Schiehallion: A Lecture to The Royal Philosophical Society of Glasgow”. 1990. http://www.sillittopages.co.uk/schie/schie90.html
[4] Davies, R. D. “A Commemoration of Maskelyne at Schiehallion”. Quarterly Journal of the Royal Astronomical Society, 26, p. 289, 1985. https://ui.adsabs.harvard.edu/abs/1985QJRAS..26..289D
[5] Danson, E. Weighing the World. Oxford University Press, 2005. ISBN 978-0-19-518169-2.
[6] Hutton, C. “An Account of the Calculations made from the Survey and Measures taken at Schehallien, in order to ascertain the mean Density of the Earth”. Philosophical Transactions of the Royal Society. 68, p. 689-788, 1778. https://doi.org/10.1098/rstl.1778.0034