What could be more simple than dropping an object and watching it fall to the ground? Our everyday experience shows that if you drop something, it falls straight down.
The Ancient Greek philosopher Aristotle used this observation to show that the Earth cannot possibly be moving or rotating. If the Earth were rotating from west to east, as some rival philosophers argued, then when you drop something, the Earth will move eastwards underneath it as it falls, and the object should land some distance west of where you dropped it! We don’t see this happening, ergo, the Earth cannot possibly be moving. Q.E.D.
Aristotle of course got many things wrong in his proposed system of the mechanics of motion and how the cosmos worked – a system known now as Aristotelian physics. Among his other contentions were that heavier objects fall faster than lighter ones, and that an object cannot undergo “unnatural motion” unless acted on by a force (falling is a “natural motion” and therefore requires no force).
One consequence of strict Aristotelian physics is that as soon as an object is released, it can have no sideways motion, and must fall straight down. This is obviously false if you observe objects such as arrows or cannonballs in flight, and natural philosophers of the Middle Ages developed the concept of impetus to explain this. The basic idea is that when a force propels an object, it implants in that object an impetus, which acts as an inherent force within the object itself, pushing it onwards. The concept took several centuries to mature, and was formalised by the French philosopher Jean Buridan in the 14th century (perhaps more famous for Buridan’s ass, which was not his backside, but a philosophical paradox).
Impetus is a forerunner of how Isaac Newton eventually solved the problem, with his idea of momentum and his Laws of Motion. Newton’s First Law says that an object at rest, or in a state of uniform motion, maintains that state unless acted on by an external force. So an object like an arrow that is fired from a bow at some speed maintains that speed unless acted on by external forces. In practice there are two forces acting on a flying arrow: air resistance, which slows down its horizontal motion, and gravity (another of Newton’s cool ideas), which causes it to begin falling towards the ground. The combination of these two results in the arrow slowing down and dropping in altitude, until eventually it hits something (either a target or the ground).
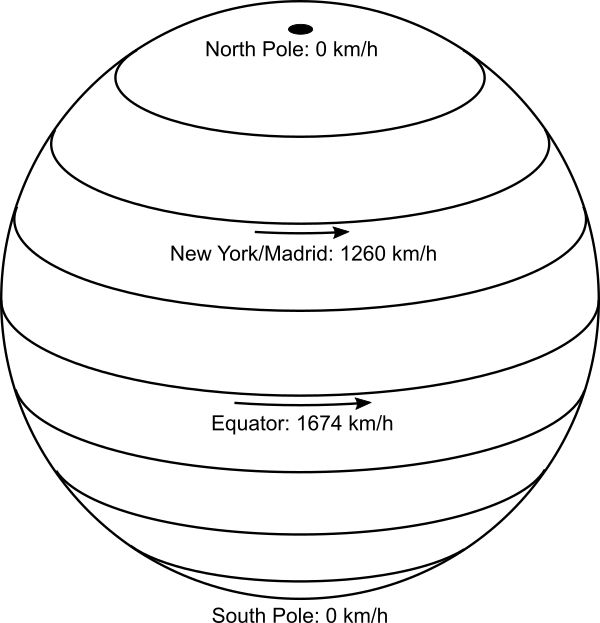
Newton’s First Law also explains why a dropped object falls straight to the ground, instead of falling to the west as the Earth rotates beneath it. An object held in your hand has the same rotational velocity as the Earth at the point where you’re standing. For example, if you’re on the equator, the rotational speed of the Earth’s surface is about 460 metres per second, so you and anything you’re holding, are moving eastwards at that speed. When you let the object go, it continues moving at 460 m/s eastward as it falls – the same speed as the Earth is moving. And so it falls at your feet, what appears to be directly downwards to you, with no sideways deflection.
Or does it?
If the Earth were flat and non-rotating, then none of this would be an issue. Objects dropped fall downwards and the non-motion of the Earth doesn’t change anything. You don’t even need Newton’s First Law.
If the Earth were flat and rotating like a record (or optical disc) about a central North Pole, things get a little more complicated. Let’s say the equator is 10,000 km from the North Pole (the same as on our Earth), and the Flat Earth rotates once per 24 hours. Then points on the equator are moving with a speed of 2π×10000/(24×60×60) km/s = 727 m/s (faster than our spherical Earth because the geometry is different). If you drop an object (and believe Newton’s laws), the object is moving east at 727 m/s and maintains that motion in a straight line as it falls. Let’s say you drop it from a height of 2 metres. It takes 0.64 seconds to hit the ground. In 0.64 seconds, the object moves east a distance of 465 metres. The ground is also moving east at 727 m/s, however, the ground is not moving in a straight line – it’s moving in a circle about the North Pole. In 0.64 seconds the ground moves through an angle of 0.0027°. Doing the trigonometry, this means the ground moves 465×cos(0.0027°) m east (which is slightly less than, but so close to 465 m that it’s not worth writing the difference) and 465×sin(0.0027°) m north, which equals 0.022 metres. So, if we live on a rotating Flat Earth, and you drop an object from 2 metres height at the equator, you should see it land 22 millimetres south of straight down.

This is a prediction of the rotating Flat Earth model. Repeating the above calculations for different latitudes (assuming distances from the North Pole equal to our round Earth), we would expect a southward deflection of 11 mm at 45° north, or 33 mm at 45° south. Do we observe such a southward deflection of falling objects? No, we don’t.
Now let’s think about our spherical Earth, because things are not quite as straightforward as they might appear. The equator is rotating at a speed of 460 m/s. It’s not moving in a straight line – it’s rotating about the Earth’s axis, once every sidereal day: T = 23 hours, 56 minutes, 4 seconds (see 36. The visible stars). The radius of rotation is the equatorial radius of the Earth: 6378.1 km. If you hold an object 2 metres above the ground, its radius of rotation is 2 metres larger, making the distance it has to travel in a sidereal day 4π metres larger. So the speed of rotation 2 metres above the ground is 4π/T = 0.000145 m/s faster than the ground. In 0.46 seconds, this means that an object 2 metres above the ground moves eastward by 0.067 millimetres greater distance than the ground does.
So if you stand on the equator and drop an object from 2 metres, it should land 0.067 mm east of straight down. If you increase the height and drop an object from 100 metres, it takes 4.52 seconds to fall and by this calculation should land 33 mm east of straight down. The German language Wikipedia has an article on this calculation (there is no English Wikipedia article on it), and derives the same result, but then it says that “a more precise calculation” produces an additional factor 2/3, citing Carl Friedrich Gauss’s collected works without any further explanation. So this gives a deflection of 22 mm for an object dropped from 100 m. There is also an adjustment for latitude, being the usual cosine(latitude) term that we have seen in many of these discussions.
This is a prediction of the rotating spherical Earth model. Do we observe such an eastward deflection of falling objects?
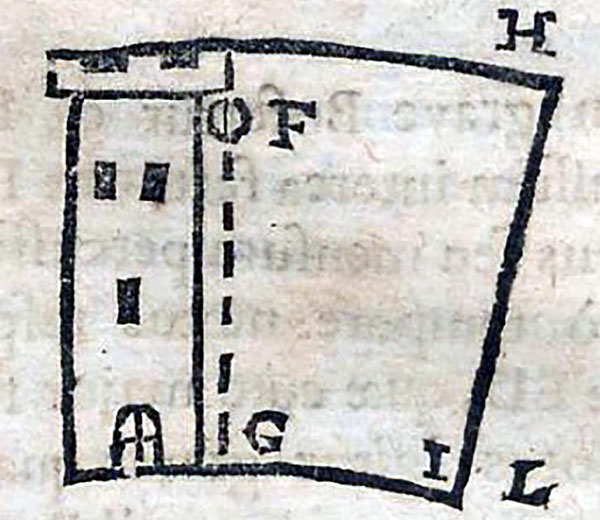
There is in fact a long history of scientists investigating this effect and trying to measure it. In 1674, the French Jesuit priest and mathematician Claude François Milliet Dechales published his Cursus seu Mondus Matematicus, which included a diagram showing the fall of an object from a tower on the rotating Earth. It’s not clear if he ever performed the experiment.
Isaac Newton himself wrote about the effect in a letter to Robert Hooke, dated 28 November, 1679, just five years later[2].
In the letter, Newton drew a diagram of an object falling, not just from a height to the ground, but continuing to fall towards the centre of the Earth (as if the object could pass through the Earth):

In the text accompanying the diagram Newton writes:
Then imagine this body be let fall and its gravity will give it a new motion towards the centre of the Earth without diminishing the previous one from west to east. Whence the motion of this body from west to east, by respect that before its fall it was more distant from the centre of the Earth than the parts of the Earth at which it arrives in its fall, will be greater than the motion from west to east of parts of the Earth at which the body arrives in its fall, and therefore it will not descend the perpendicular AC, but outrunning the parts of the Earth will shoot forward to the east side of the perpendicular, describing in its fall a spiral line ADEC.
Newton goes on to suggest that a “descent of but 20 to 30 yards” may be enough to observe the eastward deflection. Being a theoretician, Newton doesn’t seem to have done the experiment, but Hooke tried to measure the eastward deflection of an object falling from a height of 8.2 metres. From this height the expected deflection is about a quarter of a millimetre at the latitude of London—very difficult to measure—and Hooke’s results were inconclusive.
The first positive result was achieved in 1791 by Italian scientist Giovanni Battista Guglielmini. He dropped a total of 16 balls from the top of the Asinelli Tower of Bologna, a height of 78 m, comparing the landing positions to a vertical defined by a plumb-bob line. He concluded that the average eastward deflection of the balls was about 18 mm, compared to a predicted deflection of 11 mm.[3] Of course, these early experiments faced many difficulties, such as air currents, the difficulty of releasing the balls without any sideways motion, and measuring a vertical plumb line accurately.
In 1802, Johann Benzenberg dropped 32 balls from the tower of St Michael’s Church in Hamburg, 76 m high. Being at a higher latitude than Bologna, the expected eastward deflection was 8.7 mm, and Benzenberg recorded an average value of 9 mm. In 1831, Ferdinand Reich dropped lead balls 158 metres down the Drei Brüders (Three Brothers) mine shaft near Freiberg, measuring 28 mm eastward deflection, with a predicted value of 29.4 mm. In 1902 Edwin Hall performed the experiment with 948 separate drops from a height of 23 m at Harvard University, measuring an eastward deflection of 1.5 mm, compared to the predicted 1.8 mm. And Camille Flammarion dropped 144 balls from 68 m in the Pantheon in Paris, measuring a deflection of 6.3 mm, compared to the theoretical 8.1 mm.[3]
This is not an easy experiment to perform with sufficient accuracy. It is sensitive to a lot of complicating factors, particularly air currents, but the overall agreement of observation with the predictions is good. And so the measurable eastward deflection of falling objects provides us with another proof that the Earth is a (rotating) globe.
Note: I’ve talked only about the eastward deflection of falling objects. There is also a smaller predicted deflection in the north-south direction for latitudes away from the equator. That will be discussed in a future Proof.
References:
[1] Dechales, C. F. M. Cursus seu mundus mathematicus (Vol. 1), 1674.
[2] Gunther, R. T. Early Science in Oxford, Volume X, Oxford University Press, Oxford, 1920-1937. https://archive.org/details/earlyscienceinox10gunt/page/52/mode/2up
[3] Tiersten, M., Soodak, H. “Dropped objects and other motions relative to the noninertial earth”. American Journal of Physics, 68, p. 129-142, 2000. https://doi.org/10.1119/1.19385