Skyglow is the diffuse illumination of the night sky by light sources other than large astronomical objects. Sometimes this is considered to include diffuse natural sources such as the zodiacal light (discussed in a previous proof), or the faint glow of the atmosphere itself caused by incoming cosmic radiation (called airglow), but primarily skyglow is considered to be the product of artificial lighting caused by human activity. In this context, skyglow is essentially the form of light pollution which causes the night sky to appear brighter near large sources of artificial light (i.e. cities and towns), drowning out natural night sky sources such as fainter stars.
The sky above a city appears to glow due to the scattering of light off gas molecules and aerosols (i.e. dust particles, and suspended liquid droplets in the air). Scattering of light from air molecules (primarily nitrogen and oxygen) is called Rayleigh scattering. This is the same mechanism that causes the daytime sky to appear blue, due to scattering of sunlight. Although blue light is scattered more strongly, the overall colour effect is different for relatively nearby light sources than it is for sunlight. Much of the blue light is also scattered away from our line of sight, so skyglow caused by Rayleigh scattering ends up a similar colour to the light sources. Scattering off aerosol particles is called Mie scattering, and is much less dependent on wavelength, so also has little effect on the colour of the scattered light.
Despite the relative independence of scattered light on wavelength, bluer light sources result in a brighter skyglow as perceived by humans. This is due to a psychophysical effect of our optical systems known as the Purkinje effect. At low light levels, the rod cells in our retinas provide most of the sensory information, rather than the colour-sensitive cone cells. Rod cells are more sensitive to blue-green light than they are to redder light. This means that at low light levels, we are relatively more sensitive to blue light (compared to red light) than we are at high light levels. Hence skyglow caused by blue lights appears brighter than skyglow caused by red lights of similar perceptual brightness.
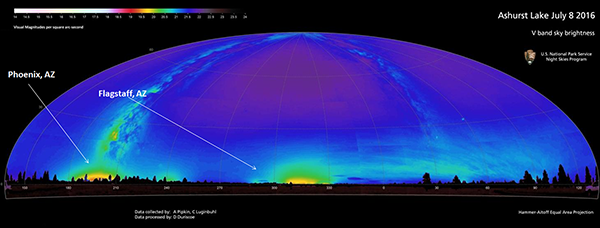
Artificially produced skyglow appears prominently in the sky above cities. It makes the whole night sky as seen from within the city brighter, making it difficult or impossible to see fainter stars. At its worst, skyglow within a city can drown out virtually all night time astronomical objects other than the moon, Venus, and Jupiter. The skyglow from a city can also be seen from dark places up to hundreds of kilometres away, as a dome of bright sky above the location of the city on the horizon.
However, although the skyglow from a city can be seen from such a distance, the much brighter lights of the city itself cannot be seen directly – because they are below the horizon. The fact that you can observe the fainter glow of the sky above a city while not being able to see the lights of the city directly is because of the curvature of the Earth.
This is not the only effect of Earth’s curvature on the appearance of skyglow; it also effects the brightness of the glow. In the absence of any scattering or absorption, the intensity of light falls off with distance from the source following an inverse square law. Physically, this is because the surface area of spherical shells of increasing radius from a light source increase as the square of the radius. So the same light flux has to “spread out” to cover an area equal to the square of the distance, thus by the conservation of energy its brightness at any point is proportional to one divided by the square of the distance. (The same argument applies to many phenomena whose strengths vary with distance, and is why inverse square laws are so common in physics.)
Skyglow, however, is also affected by scattering and absorption in the atmosphere. The result is that the brightness falls off more rapidly with distance from the light source. In 1977, Merle F. Walker of Lick Observatory in California published a study of the sky brightness caused by skyglow at varying distances from several southern Californian cities[1]. He found an empirical relationship that the intensity of skyglow varies as the inverse of distance to the power of 2.5.

This relationship, known as Walker’s law, has been confirmed by later studies, with one notable addition. It only holds for distances up to 50-100 kilometres from the city. When you travel further away from a city, the intensity of the skyglow starts to fall off more rapidly than Walker’s law suggests, a little bit faster at first, but then more and more rapidly. This is because as well as the absorption effect, the scattered light path is getting longer and more complex due to the curvature of the Earth.
A later study by prominent astronomical light pollution researcher Roy Henry Garstang published in 1989 examined data from multiple cities in Colorado, California, and Ontario to produce a more detailed model of the intensity of skyglow[2]. The model was then tested and verified for multiple astronomical sites in the mainland USA, Hawaii, Canada, Australia, France, and Chile. Importantly for our perspective, the model Garstang came up with requires the Earth’s surface to be curved.
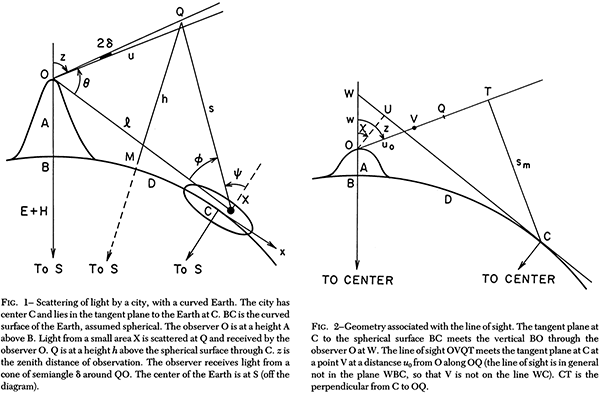
Interestingly, Garstang also calculated a model for the intensity of skyglow if you assume the Earth is flat. He did this because it greatly simplifies the geometry and the resulting algebra, to see if it produced results that were good enough. However, quoting directly from the paper:
In general, flat-Earth models are satisfactory for small city distances and observations at small zenith distances. As a rough rule of thumb we can say that for calculations of night-sky brightnesses not too far from the zenith the curvature of the Earth is unimportant for distances of the observer of up to 50 km from a city, at which distance the effect of curvature is typically 2%. For larger distances the curved-Earth model should always be used, and the curved-Earth model should be used at smaller distances when calculating for large zenith distances. In general we would use the curved-Earth model for all cases except for city-center calculations. […] As would be expected, we find that the inclusion of the curvature of the Earth causes the brightness of large, distant cities to fall off more rapidly with distance than for a flat-Earth model.
In other words, to get acceptably accurate results for either distances over 50 km or for large zenith angles at any distance, you need to use the spherical Earth model – because assuming the Earth is flat gives you a significantly wrong answer.
This result is confirmed experimentally again in a 2007 paper[3], as shown in the following diagram:
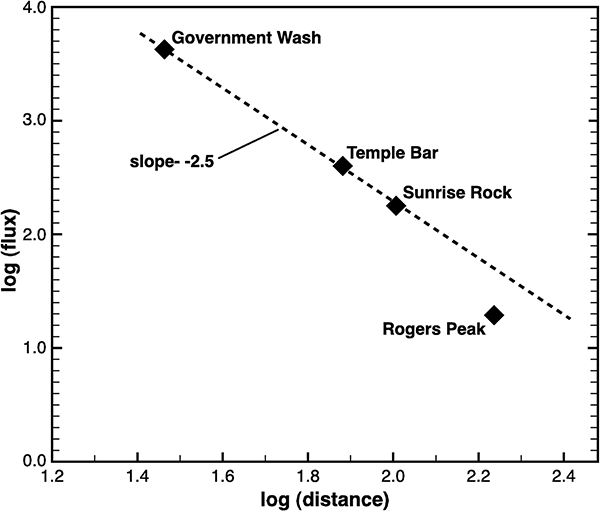
So astronomers, who are justifiably concerned with knowing exactly how much light pollution from our cities they need to contend with at their observing sites, calculate the intensity of skyglow using a model that is significantly more accurate if you include the curvature of the Earth. Using a flat Earth model, which might otherwise be preferred for simplicity, simply isn’t good enough – because it doesn’t model reality as well as a spherical Earth.
References:
[1] Walker, M. F. “The effects of urban lighting on the brightness of the night sky”. Publications of the Astronomical Society of the Pacific, 89, p. 405-409, 1977. https://doi.org/10.1086/130142
[2] Garstang, R. H. “Night sky brightness at observatories and sites”. Publications of the Astronomical Society of the Pacific, 101, p. 306-329, 1989. https://doi.org/10.1086/132436
[3] Duriscoe, Dan M., Luginbuhl, Christian B., Moore, Chadwick A. “Measuring Night-Sky Brightness with a Wide-Field CCD Camera”. Publications of the Astronomical Society of the Pacific, 119, p. 192-213, 2007. https://dx.doi.org/10.1086/512069


So are you saying that skyglow is actually good for something?
Comparing to Wikipedia, “442 and 540 nanometres respectively” appears to be in the wrong order.
It’s so easy to transpose two random numbers like that… fixed, thanks!
>it also effects the brightness of the glow
This means that it brings about the brightness; that without it, the glow wouldn’t be bright. You mean to say that it *affects* the brightness.