[audio version of this article]
We’re all familiar with the horizon. Informally, the horizon is as far as you can see, where the sky apparently meets the ground. The horizon of the Earth will come up in several of the proofs we’ll be looking at, but today we’ll be looking at one specific property of the horizon.
Firstly, we need to define our terms more precisely, and recognise that there are three different types of horizon. For the first type, the horizon is defined by a plane perpendicular to the direction of up and down. Up and down are defined by the direction of gravity. If we’re standing on the surface of Earth, then the force of gravity has a specific direction, which we call down. Now look exactly perpendicular to this direction. You can spin on the spot, looking perpendicular to the down direction at all times. This defines a horizontal plane; indeed the very word “horizontal” is derived from “horizon”. This horizon you are looking at is called the astronomical horizon. It might also sensibly be called the geometric or mathematical horizon.
Now let’s define the horizon in a different way. Imagine standing on the surface of the Earth, in a relatively flat area such as an open plain, or perhaps looking out to sea. Look in the direction of the apparent line where the sky meets the Earth’s surface. This is what most people usually think of when they think of “the horizon”, and this is called the true horizon.
A third type of horizon occurs when you’re standing in a place where the landscape is not particularly flat. The true horizon might be obscured by mountains or trees or buildings or whatever. In this case, as far as you can see is called the visible horizon. If the visible horizon obscures the true horizon, then the obstructions need to be projecting above the notionally smooth surface of the Earth, so the visible horizon must be higher and closer than the true horizon (or at the same place as the true horizon if there are no obstructions).
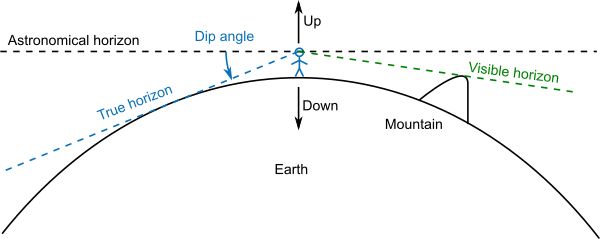
Let’s think about the case where there are minimal obstructions and the visible horizon is more or less the same as the true horizon. Now the question arises: Is the true horizon the same as the astronomical horizon, or different?
If the Earth is flat, the astronomical horizon is a plane parallel to the (flat) ground, at the height of the human observer’s eyes. The true horizon is the plane of the Earth itself. These two planes run parallel and, by the laws of perspective, appear to converge at infinity. So if you look horizontally (i.e. in the direction of the astronomical horizon), you will see the true horizon in the same direction.
On the other hand, if the Earth is spherical, the Earth’s surface curves downwards, away from the plane of the astronomical horizon. So there should be a non-zero angle between the directions of the astronomical and true horizons. This angle is called the dip angle of the horizon. For a person standing on the ground, this angle is very small and mostly imperceptible. But you can measure the dip angle with a surveyor’s theodolite or its less technological predecessor, an astrolabe. And as your elevation increases, the dip angle increases as well. If you make these measurements with an instrument, you can verify that the dip angle is non-zero, and that it increases with the elevation of your observing position.
The 11th century Persian scholar Abū Rayḥān Muḥammad ibn Aḥmad Al-Bīrūnī (usually known in English as Al-Biruni) recognised all of this, and what’s more he realised that by measuring the dip angle of the horizon from a known elevation he could do the geometry and calculate the circumference of the Earth. Eratosthenes beat him to it, but Al-Biruni’s method was arguably more clever, and could be done without needing measurements at different cities.
First, Al-Biruni measured the height of a mountain near where he lived. He did this by sighting two elevation angles to the top of the mountain from different distances, and solving the geometry to get the height. Then he climbed the mountain and measured the dip angle of the horizon. From the height, the dip angle, and some basic geometry, Al-Biruni could calculate the circumference of the Earth.

Given the geometry in the figure, some straightforward trigonometry shows that the radius of the Earth is given by the expression:
R = h(cos θ) / (1 – cos θ)
The circumference is just 2π times the radius, so:
Earth’s circumference = 2πh(cos θ) / (1 – cos θ)
How close did Al-Biruni get? Here’s where things get a little fuzzy. There are claims that he got the correct answer to within about 20 kilometres, significantly more accurate than Eratosthenes’ measurement. But these claims are disputed, partly for reasons similar to Eratosthenes’ result: nobody seems to be sure of the conversion factor from Persian cubits to modern units of distance. There are also claims that atmospheric refraction effects in the hot Persian desert would make measuring the angle correctly difficult, if not impossible.
What is the truth here? At this point far removed in history it seems almost impossible to tell. Did Al-Biruni even make the actual measurement? This raises a question about how much we trust historical accounts of scientific activities and experiments. In the case of Eratosthenes, we have multiple sources that agree on what he did, and the tradition of written literature from the Classical Greek period to the present day is more or less continuous and argued by scholars to be mostly reliable. For Al-Biruni, the evidence is less clear.
However, whether or not these historical figures actually made the measurements they are credited with is much less important for science than it is for history. History is the study of what happened in our past. Due to incomplete or unreliable record keeping, history can, alas, be lost. Science, in contrast, is the study of the universe and the laws of nature. Scientific experiments, by their very nature, are repeatable. Even if Eratosthenes or Al-Biruni never made the measurements, we can reproduce the methods and come up with the same answers (to within the care and accuracy of our experiments).
What does seem reasonably certain is that Al-Biruni did the geometry, providing us with another method of demonstrating that the Earth is not flat. We don’t have to take anyone’s word for it that he did the experiment and showed that the Earth is spherical, because we can do it ourselves.
There are a couple of ways of doing this experiment. The traditional way is with a theodolite. Surveying theodolites have an accurate levelling mechanism. Once the level is set, the theodolite can measure the vertical angle to any object you sight through the telescope eyepiece. Just sight the line of the horizon and read off the dip angle.
If you don’t happen to have a theodolite, there are smartphone apps available that use the phone’s GPS and inclinometer systems to provide navigation or surveying aids, including an artificial horizon indicator. The phone’s inclinometer measures the direction of gravity, so the app can easily plot the astronomical horizon. This is displayed on your phone screen, overlaid on a photo from the phone’s camera.
If you calibrate and check the app at sea level, you can see that the astronomical horizon is very close to the true horizon – the angle between them is too small to notice or measure easily. But on a mountain or on a flight, you can capture a photo of the horizon—where the ground or layers of clouds below you meet the blue sky‒overlaid with the artificial astronomical horizon. You can see the angle between them and measure it with the app. And if you know your altitude, which you can also get from the GPS reading on the app, or by checking in-flight data, you can calculate the circumference of the Earth yourself. In theory.
In practice there are a few complicating factors. The inclinometers in phones are not especially accurate and can be thrown out by forces in flight when turning or changing altitude. And the Earth’s atmosphere refracts light, so sighting very distant objects can give inaccurate angles. So although you can see that the true horizon is lower than the astronomical horizon, calculating the Earth’s circumference in this way can easily give an incorrect value. What this teaches us is that when doing scientific experiments, we have to be aware of any factors that can bias our measurements, and try to eliminate them or correct for them. This is a common theme through the history of science: Not only does our understanding grow, but our ability to understand and correct for complicating factors becomes more sophisticated as well.

I like this proof. It’s all well and good to say, as you did in #1, that you can see the curvature of Earth for yourself … from space. But you can see it for yourself right here on the ground! You just have to look very closely.
“… more less technological … “?
Signed, nitpicking.com.
Oops! Fixed, thanks.
“What this teaches us is that when doing scientific experiments, we have to be aware of any factors that can bias our measurements, and try to eliminate them or correct for them.” This statement right here is fundamental to our understanding of the learning experience. You nailed it.Not only be aware of the other factors but be willing to revisit the experiment, possibly again and again, to learn even more. Do not become to pompous or full of ourselves to think we know everything. Stand it back up, turn it around, look at it from a different angle. Thanks and continue perusing the cat theory.
Do we have anybody here near a high seaside mountain, such as Table Mountain in Cape Town? None of the hills near me have a good true horizon.
And I suppose it would be worth checking what the standard correction for atmospheric refraction is. If I recall correctly, that was usually printed in the tables used for celestial navigation, back in the day when every ship carried a sextant.
There’s a lookout near me with views over the Pacific Ocean. It’s… (checks)… 155 metres elevation. Not enormous. I could probably find somewhere a little bit higher, but the geography here is quite flat.
The visible horizon can be below the true horizon if you are on the rim of a wide valley.
The curvature of the earth affects the described method for measuring the height of the mountain. But this effect is minor.
… and can be corrected for.
So this evidence bumps up against the complication of refraction effects, making it a suitable place to mention “looming and similar refraction phenomena” [0].
As I understand it, the way the flat-earthers dodge the story of the horizon, and indeed of the sun setting, while remaining in plain view always for roughly half the world, is by claiming that light bends *upwards* away from the Earth; that is, a ray leaving the top of a mountain horizontally bends slowly upwards until it leaves the atmosphere at a diagonal; and, likewise, light from any shallower diagonal bends upwards as it approaches the Earth’s surface until it reaches horizontal higher above ground level than the top of that mountain and then curves back up and away. So they account for the setting sun by saying it’s gone far enough away that the angle to it is below the critical angle at which such curvature would deflect it away to pass above our heads – and, indeed, above the clouds we can see. Only those for whom the true direction to The Sun is more than a certain critical angle can then see it above their apparent horizon.
This, of course, requires an effect that causes the up-curving well above the highest clouds (so that, before a ray approaching the high clouds can hit them, it has bent upwards); which, given any atmospheric model capable of balancing the weight air above by the pressure at each altitude, means the curvature must happen even when the atmosphere is very rarefied. This, in turn, means it must be a non-atmospheric effect associated simply with altitude; which, of course, smacks of exceptionalism, but tell me something new about flat-earther hypotheses.
Now orthodoxy also has curvature of light paths – due to refraction as a result of variation in the atmosphere’s properties; but that involves the light curving down, not up. This fits with what we know of refraction (so no exceptionalism here): more or less, the thicker the air, the slower the light, the higher the refractive index. Since lower altitudes have thicker air (higher pressure increases density, as does higher humidity; and, while density isn’t actually the decisive factor, it’s a tolerably good surrogate; for real precision, do experiments) they have higher refractive index then higher altitude, which is exactly the condition that’ll cause downward curvature.
That’s established physics that we can show in a lab at sea level; split a box, with vertical glass plates (of uniform thickness) parallel to one of its faces, into sub-chambers, each with a top that can be pushed down on with variable force, to cause the pressures in the chambers to vary; shine light horizontally (to eliminate any putative disturbance from the up-curving special physics) through the chambers at an angle to the dividing planes and look at the angles the light makes as it passes from chamber to chamber; vary the pressures in the chambers; observe that light passing from a high pressure chamber to a lower-pressure chamber makes a closer-to-perpendicular angle to the glass plate in the higher pressure chamber. Reverse the pressure variation (to eliminate the possibility of the result being due to imperfections in the set-up) and observe the angles flipping to the other way round.
The flath-earthers thus need their upwards curvature to more than compensate for the refractive index tending to make light curve down. OK, so they just tweak their parameters, or something – they exempt their own views from any principle of parsimony, so arbitrary amounts of parameter-tweaking only ever strike them as a problem with other folk’s theories, never their own claims. None the less, they should be required to make their model’s parameters explicit, so that they can actually be compared with experiment.
I have a suspicion they’ve left that wilfully vague, precisely to be safe from such a test; but it might be possible to prove that no model of the kind sketched can actually be made to work.
Looming (e.g. the Novaya Zemlya effect) involves seeing The Sun (or some other astronomical body, or some distant geography) when it “should” be below the horizon, due to the refractive index gradient in the atmosphere being stronger than usual. The flatties can presumably then argue that the refractive effect is overcoming the up-curve effect more than usual, to let one see “closer to horizontal” (where orthodoxy says we’re seeing further below horizontal).
I wonder whether that contrivance can actually survive exact analysis, though.
[0] https://en.wikipedia.org/wiki/Looming_and_similar_refraction_phenomena
Thinking about it, the killer argument against the “light bends up” theory is of course the fact that stars keep their relative positions consistently as they wheel across the sky, with small perturbations when near the horizon, that indicate orthodoxy’s down-bending – rather than up-bending.