Earth’s atmosphere is held on by gravity, pulling it towards the centre of the planet. This means the air can move sideways around the planet in a relatively unrestricted manner, creating wind and weather systems, but it has trouble flying upwards into space.
It is possible for a planet’s atmosphere to leak away into space, if the gravity is too weak to hold it. Planets have an escape velocity, which is the speed at which an object fired directly upwards must have in order for it to fly off into space, rather than slow down and fall back down. For Earth, this escape velocity is 11.2 km/s. Almost nothing on Earth goes this fast – but there are some things that do. Gas molecules.
Air is made up of a mixture of molecules of different gases. The majority, around 78%, is nitrogen molecules, made of two atoms of nitrogen bonded together, followed by 21% oxygen molecules, similarly composed of two bonded oxygen atoms. Almost 1% is argon, which is a noble gas, its atoms going around as unbonded singletons. Then there are traces of carbon dioxide, helium, neon, methane, and a few others. On top of these is a variable amount of water vapour, which depending on local weather conditions can range from almost zero to around 3% of the total.
Gas is the state of matter in which the component atoms and molecules are separated and free to move mostly independently of one another, except for when they collide. This contrasts with a solid, in which the atoms are rigidly connected, a liquid, in which the atoms are in close proximity but able to flow and move past one another, and a plasma, in which the atoms are ionised and surrounded by a freely moving electrically charged cloud of electrons. The deciding factors on which state a material exists in are temperature and pressure.
Temperature is a measurable quantity related to the amount of thermal energy in an object. This is the form of energy which exists in the individual motion of atoms and molecules. In a solid, the atoms are vibrating slightly. As they increase in thermal energy they vibrate faster, until the energy breaks the bonds holding them together, and they form molecules and start to flow, becoming a liquid. As the temperature rises and more thermal energy is added, the molecules begin to fly off the mass of liquid completely, dispersing as a gas. And if more energy is added, it eventually strips the outer electrons off the atoms, ionising the gas into a plasma.
The speed at which molecules move in a gas is determined by the relationship between temperature and the kinetic energy of the molecules. The equipartition theorem of thermodynamics says that the average kinetic energy of molecules in a gas is equal to (3/2)kT, where T is the temperature and k is the Boltzmann constant. If T is measured in kelvins, the Boltzmann constant is about 1.38×10-23 joules per kelvin. So the kinetic energy of the molecules depends linearly on the temperature, but kinetic energy equals (1/2)mv2, where m is the mass of a molecule and v is the velocity. So the average speed of a gas molecule is then √(3kT/m). This means that more massive molecules move more slowly.
For example, here are the molecular masses of some gases and the average speed of the molecules at room temperature:
| Gas | Molecular mass (g/mol) | Average speed (m/s) |
|---|---|---|
| Hydrogen (H2) | 2.016 | 1920 |
| Helium | 4.003 | 1362 |
| Water vapour (H2O) | 18.015 | 642 |
| Neon | 20.180 | 607 |
| Nitrogen (N2) | 28.014 | 515 |
| Oxygen (O2) | 32.000 | 482 |
| Argon | 39.948 | 431 |
| Carbon dioxide (CO2) | 44.010 | 411 |
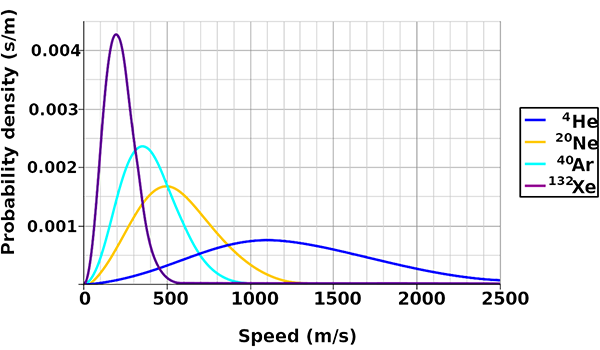
Remember that these are the average speeds of the gas molecules. The speeds actually vary according to a statistical distribution known as the Maxwell-Boltzmann distribution. Most molecules have speeds around the average, but there are some with lower speeds all the way down to zero, and some with higher speeds. At the upper end, the speed distribution is not limited (except by the speed of light), although very few molecules have speeds more than 2 or 3 times the average.
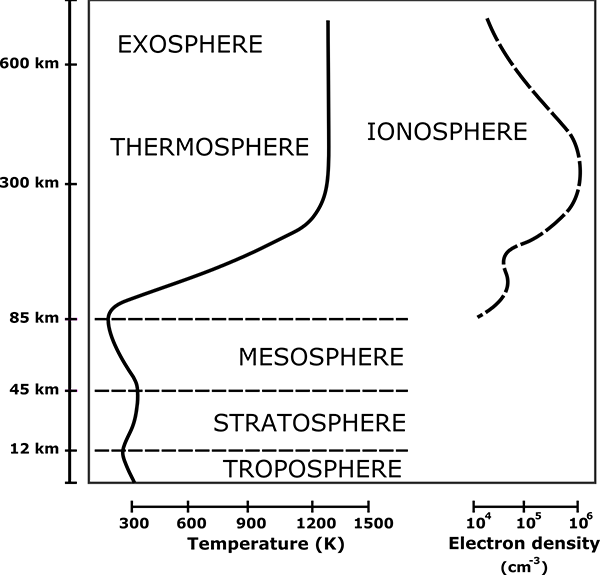
These speeds are low enough that essentially all the gas molecules are gravitationally bound to Earth. At least in the lower atmosphere. As you go higher the air rapidly gets thinner—because gravity is pulling it down to the surface—but the pressure means it can’t all just pile up on the surface, so it spreads ever thinly upwards. The pressure drops exponentially with altitude: at 5 km the pressure is half what it is at sea level, at 10 km it’s one quarter, at 15 km one eighth, and so on.
The physics of the atmosphere changes as it moves to higher altitudes and lower pressures. Some 99.998% of the atmosphere by mass is below 85 km altitude. The gas above this altitude, in the thermosphere and exosphere, is so rarefied that it is virtually outer space. Incoming solar radiation heats the gas and it is so thin that heat transport to lower layers is inefficient and slow. Above about 200 km the gas temperature is over 1000 K, although the gas is so thin that virtually no thermal energy is transferred to orbiting objects. At this temperature, molecules of hydrogen have an average speed of 3516 m/s, and helium 2496 m/s, while nitrogen is 943 m/s.
While these average speeds are still well below the escape velocity, a small fraction of molecules at the high end of the Maxwell-Boltzmann distribution do have speeds above escape velocity, and if moving in the right direction they fly off into space, never to return to Earth. Our atmosphere leaks hydrogen at a rate of about 3 kg/s, and helium at 50 g/s. The result of this is that any molecular hydrogen in Earth’s atmosphere leaks away rapidly, as does helium.
There is virtually no molecular hydrogen in Earth’s atmosphere. Helium exists at an equilibrium concentration of about 0.0005%, at which the leakage rate is matched by the replacement of helium in the atmosphere produced by alpha decay of radioactive elements. Recall that in alpha decay, an unstable isotope emits an alpha particle, which is the nucleus of a helium atom. Radioactive decay is the only source of helium we have. Decaying isotopes underground can have their alpha particles trapped in petroleum and natural gas traps underground, creating gas reservoirs with up to a few percent helium; this is the source of all helium used by industry. Over the billions of years of Earth’s geological history, it has only built up enough helium to last our civilisation for another decade or two. Any helium that we use and is released to the atmosphere will eventually be lost to space. It will become increasingly important to capture and recycle helium, lest we run out.
Because of the rapid reduction in probabilities for high speeds of the Maxwell-Boltzmann distribution, the leakage rate for nitrogen, oxygen, and heavier gases is much slower. Fortunately for us, these gases leak so slowly from our atmosphere that they take billions of years for any appreciable loss to occur.
This is the case for a spherical Earth. What if the Earth were flat? Well, the atmosphere would spill over the sides and be lost in very quick time. But wait, a common feature of flat Earth models is impassable walls of ice near the Antarctic rim to keep adventurous explorers (and presumably animals) from falling off the edge. Is it possible that such walls could hold the atmosphere in?
If they’re high enough, sure! Near the boundary between the thermosphere and the exosphere, the gas density is extremely low, and most (but not all) of the molecules that make it this high are hydrogen and helium. If the walls were this high, it would stop virtually all of the nitrogen and oxygen from escaping. However, if the walls were much lower, nitrogen and oxygen would start leaking at faster and faster rates. So how high do the walls need to be? Roughly 500-600 kilometres.
That’s well and truly impassable to any explorer using anything less than a spacecraft, so that’s good. But walls of ice 500 km high? We saw when discussing hydrostatic equilibrium that rock has the structural strength to be piled up only around 10 km high before it collapses under its own gravity. The compressive strength of ice, however, is of the order 5-25 megapascals[1][2], about a tenth that of granite.
Ice is also less dense than rock, so a mountain of ice has a lot less mass than a mountain of granite. However, doing the sums shows that an Everest-sized pile of ice would produce a pressure of 30 MPa at its base, meaning it would collapse under its own weight. And that’s more than 50 times shorter than the walls we need to keep the atmosphere in.
So the fact that we can breathe is a consequence of our Earth being spherical. If it were flat, there would be no physically plausible way to keep the atmosphere in. (There are other models, such as the Earth being covered by a fixed firmament, like a roof, to which the stars are affixed, but these have even more physical problems – which will be discussed another day.)
References:
[1] Jones, S. J. “The confined compressive strength of polycrystalline ice”. Journal of Glaciology, 28 (98), p. 171-177, 1982. https://doi.org/10.1017/S0022143000011874
[2] Petrovic, J. J. “Review: Mechanical properties of ice and snow”. Journal of Materials Science, 38, p. 1-6, 2003. https://doi.org/10.1023/A:1021134128038
Also, a 500km-high structure on a flat surface?
That would be something you could see from a veeery long distance, despite the efforts of the Illuminati police that patrols the Antartica “ring”.
Excellent point – I should have thought of that! 🙂
Just two things to quibble about. First, you implicitly assume that in a flat earth model, whatever mechanism which accounts for gravity allows for things to fall off the edge. There are some which wouldn’t allow that, like models with a firmament.
The second is actually something of consequence, though; that’s your usage of “heat”. The technical definition of heat is that it is a process of energy exchange, much like work. Just as you wouldn’t say there is work in an object or a system, you shouldn’t say that there is heat in an object or a system. It’s an unfortunate quirk of language resulting from naming things before understanding them. Temperature is related to the amount of thermal energy (some will call this internal energy). We can increase temperature by doing heat on a system.
I am fully aware that most people would say “adding heat to a system” instead of “doing heat on a system”. This is not me trying to proscribe a narrow definition because I think I’m smarter than everyone else. The fact is that many people struggle to conceptually understand thermodynamics generally, and heat in particular, and I believe that a lot of that struggle comes from preconceived notions about what heat is, related to the way that heat is talked about. If people talked about heat in the same way that we talk about work (in technical settings, at least), that would go a long way to preventing those struggles before they happen.
Language is shaped by the people who use it, and I’m advocating (not proscribing) for this usage.
Thanks for the comments. Thermodynamics isn’t my specialty area of physics, so I guess I was a little sloppy with the technical definition of heat. I’ll revise the text to use “thermal energy”.
And yes, I neglected a firmament model, I should mention that too.
If you want to say ‘do’ instead of ‘add’ (which is a very reasonable thing to want) in a way that fits well with English grammar, then you can say ‘do heating’. Unless you *want* to jar our sense of grammar so that we realize the problem with how that grammar treats ‘heat’.
Basically, the problem is that “heat” is treated grammatically differently than “work”, and the only way to alleviate that is to treat “heat” and “work” as grammatically equivalent. So, while it’s not the *goal* to jar one’s sense of grammar, it is a necessitated outcome. I don’t want to use “do” instead of “add”, I want to be able to interchange “work” and “heat” and have the sentence still make grammatical sense.
I guess that my point is that you can interchange the words ‘work’ and ‘heating’. Arguably, the noun ‘heat’ should never be used; the colloquial meaning is more like temperature, and what people thought that they meant when they began to use it in a technical sense turned out not to exist. But the *verb* ‘heat’ means just what it should mean, and it gives rise to the gerund noun ‘heating’. (You can even say ‘heat’ (the verb) instead of ‘do heat’, but then you don’t get the contrast with work.)
My point is that, when we are restricted to using the technical terms, “work” and “heat” are technically defined such that they play the exact same grammatical roles, and you would be better off getting comfortable with that because it will give you a better understanding of what heat means, rather than trying to cling to archaic language that was built off an incomplete and at times incorrect understanding simply because this accident of language is comfortable.
As far as the colloquial terms go, language is dumb. There are words which are their own antonym! That should not happen; logically, you can’t have something be both what it is and what it isn’t. But language isn’t logical, and words can have multiple meanings. Once we’ve restricted ourselves to the technical, thermodynamic meaning, however, then we have the rigidity which allows for the sort of argument I’m making.
Simply put, I’m arguing that we should keep the definition as-is and change how we feel about the word. You are arguing that we should change the definition so we can keep how we feel about the word intact. And you’re not going to convince me to put your feelings above the established definition of the word.