In our last entry on neutrino beams, we met James Chadwick, who discovered the existence of the neutron in 1932. The neutron explained radioactive beta decay as a process in which a neutron decays into a proton, an electron, and an electron antineutrino. This also means that a reverse process, known as electron capture, is possible: a proton and an electron may combine to form a neutron and an electron neutrino. This is sometimes also known as inverse beta decay, and occurs naturally for some isotopes with a relative paucity of neutrons in the nucleus.
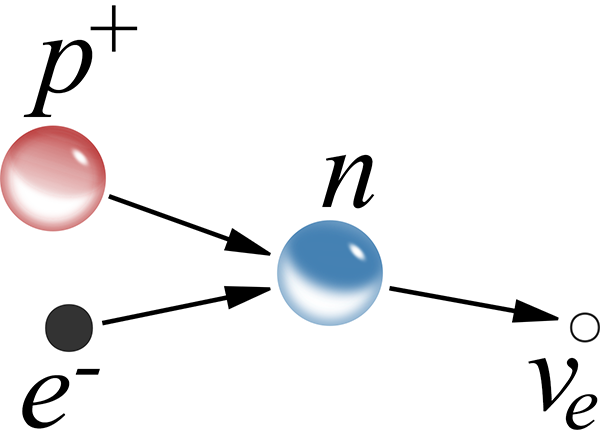
In most circumstances though, an electron will not approach a proton close enough to combine into a neutron, because there is a quantum mechanical energy barrier between them. The electron is attracted to the proton by electromagnetic force, but if it gets too close then its position becomes increasingly localised and by Heisenberg’s uncertainty principle its energy goes up correspondingly. The minimum energy state is the orbital distance where the electron’s probability distribution is highest. In electron capture, the weak nuclear force overcomes this energy barrier.
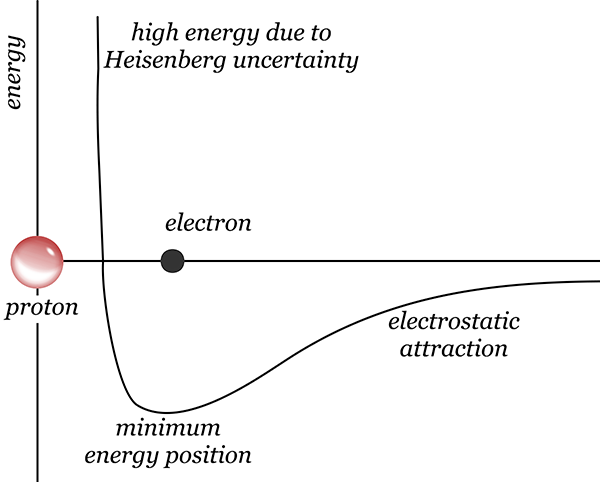
But you can also overcome the energy barrier by providing external energy in the form of pressure. Squeeze the electron and proton enough and you can push through the energy barrier, forcing them to combine into a neutron. In 1934 (less than 2 years after Chadwick discovered the neutron), astronomers Walter Baade and Fritz Zwicky proposed that this could happen naturally, in the cores of large stars following a supernova explosion (previously discussed in the article on supernova 1987A).
During a star’s lifetime, the enormous mass of the star is prevented from collapsing under its own gravity by the energy produced by nuclear fusion in the core. When the star begins to run out of nuclear fuel, that energy is no longer sufficient to prevent further gravitational collapse. Small stars collapse to a state known as a white dwarf, in which the minimal energy configuration has the atoms packed closely together, with electrons filling all available quantum energy states, so it’s not possible to compress the matter further. However, if the star has a mass greater than about 1.4 times the mass of our own sun, then the resulting pressure is so great that it overwhelms the nuclear energy barrier and forces the electrons to combine with protons, forming neutrons. The star collapses even further, until it is essentially a giant ball of neutrons, packed shoulder to shoulder.
These collapses, to a white dwarf or a so-called neutron star, are accompanied by a huge and sudden release of gravitational potential energy, which blows the outer layers of the star off in a tremendously violent explosion, which is what we can observe as a supernova. Baade and Zwicky proposed the existence of neutron stars based on the understanding of physics at the time. However, they could not imagine any method of ever detecting a neutron star. A neutron star would, they imagined, simply be a ball of dead neutrons in space. Calculations showed that a neutron star would have a radius of about 10 kilometres, making them amazingly dense, but correspondingly difficult to detect at interstellar distances. So neutron stars remained nothing but a theoretical possibility for decades.
In July 1967, Ph.D. astronomy student Jocelyn Bell was observing with the Interplanetary Scintillation Array at the Mullard Radio Astronomy Observatory in Cambridge, under the tutelage of her supervisor Antony Hewish. She was looking for quasars – powerful extragalactic radio sources which had recently been discovered using the new observation technique of radio astronomy. As the telescope direction passed through one particular patch of sky in the constellation of Vulpecula, Bell found some strange radio noise. Bell and Hewish had no idea what the signal was. At first they assumed it must be interference from some terrestrial or known spacecraft radio source, but over the next few days Bell noticed the signal appearing 4 minutes earlier each day. It was rising and setting with the stars, not in synch with anything on Earth. The signal was from outside our solar system.
Bell suggested running the radio signal strength plotter at faster speeds to try to catch more details of the signal. It took several months of persistent work, examining kilometres of paper plots. Hewish considered it a waste of time, but Bell persisted, until in November she saw the signal drawn on paper moving extremely rapidly through the plotter. The extraterrestrial radio source was producing extremely regular pulses, about 1 1/3 seconds apart.
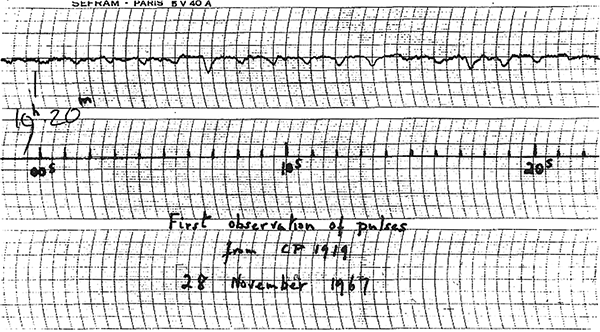
This was exciting! Bell and Hewish thought that it might possibly be a signal produced by alien life, but they wanted to test all possible natural sources before making any sort of announcement. Bell soon found another regularly pulsating radio source in a different part of the sky, which convinced them that it was probably a natural phenomenon.
They published their observations[2], speculating that the pulses might be caused by radial oscillation in either white dwarfs or neutron stars. Fellow astronomers Thomas Gold and Fred Hoyle, however, immediately recognised that the pulses could be produced by the rotation of a neutron star.
Stars spin, relatively leisurely, due to the angular momentum in the original clouds of gas from which they formed. Our own sun rotates approximately once every 24 days. During a supernova explosion, as the core of the star collapses to a white dwarf or neutron star, the moment of inertia reduces in size and the rotation rate must increase correspondingly to conserve angular momentum, in the same way that a spinning ice skater speeds up by pulling their arms inward. Collapsing from stellar size down to 10 kilometres produces an increase in rotation rate from once per several days to the incredible rate of about once per second. At the same time, the star’s magnetic field is pulled inward, greatly strengthening it. Far from being a dead ball of neutrons, a neutron star is rotating rapidly, and has one of the strongest magnetic fields in nature. And when a magnetic field oscillates, it produces electromagnetic radiation, in this case radio waves.
The magnetic poles of a neutron star are unlikely to line up exactly with the rotational axis. Radio waves are generated by the rotation and funnelled out along the magnetic poles, forming beams of radiation. So as the neutron star rotates, these radio beams sweep out in rotating circles, like lighthouse beacons. A detector in the path of a radio beam will see it flash briefly once per rotation, at regular intervals of the order of one second – exactly what Bell observed.
Radio-detectable neutron stars quickly became known as pulsars, and hundreds more were soon detected. For the discovery of pulsars, Antony Hewish was awarded the Nobel Prize in Physics in 1974, however Jocelyn Bell (now Jocelyn Bell Burnell after marriage) was overlooked, in what has become one of the most notoriously controversial decisions ever made by the Nobel committee.
Astronomers found pulsars in the middle of the Crab Nebula supernova remnant (recorded as a supernova by Chinese astronomers in 1054), the Vela supernova remnant, and several others, cementing the relationship between supernova explosions and the formation of neutron stars. Popular culture even got in on the act, with Joy Division’s iconic 1979 debut album cover for Unknown Pleasures featuring pulse traces from pulsar B1919+21, the very pulsar that Bell first detected.
By now, the strongest and most obvious pulsars have been discovered. To discover new pulsars, astronomers engage in pulsar surveys. A radio telescope is pointed at a patch of sky and the strength of radio signals received is recorded over time. The radio trace is noisy and often the pulsar signal is weaker than the noise, so it’s not immediately visible like B1919+21. To detect it, one method is to perform a Fourier transform on the signal, to look for a consistent signal at a specific repetition period. Unfortunately, this only works for relatively strong pulsars, as weak ones are still lost in the noise.
A more sensitive method is called epoch folding, which is performed by cutting the signal trace into pieces of equal time length and summing them all up. The noise, being random, tends to cancel out, but if a periodic signal is present at the same period as the sliced time length then it will stack on top of itself and become more prominent. Of course, if you don’t know the period of a pulsar present in the signal, you need to try doing this for a large range of possible periods, until you find it.
To further increase the sensitivity, you can add in signals recorded at different radio frequencies as well – most radio telescopes can record signals at multiple frequencies at once. A complication is that the thin ionised gas of the interstellar medium slows down the propagation of radio waves slightly, and it slows them down by different amounts depending on the frequency. So as the radio waves propagate through space, the different frequencies slowly drift out of synch with one another, a phenomenon known as dispersion. The total amount of dispersion depends in a known way on the amount of plasma travelled through—known as the dispersion measure—so measuring the dispersion of a pulsar gives you an estimate of how far away it is. The estimate is a bit rough, because the interstellar medium is not uniform – denser regions slow down the waves more and produce greater dispersion.
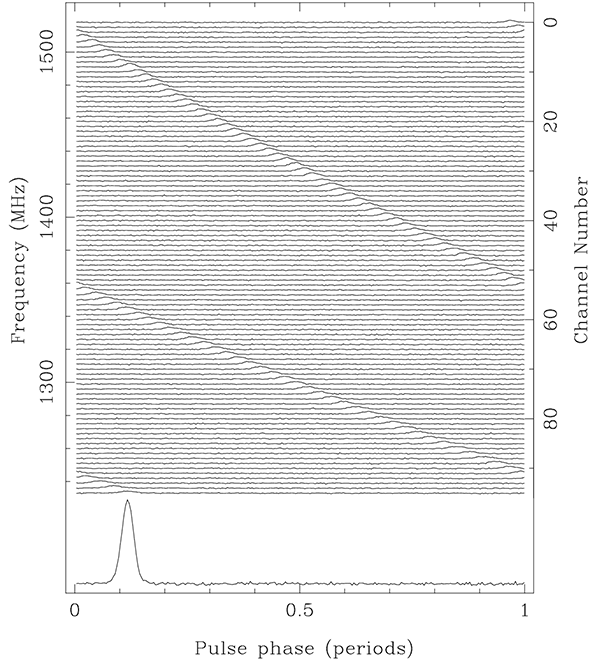
So to find a weak pulsar of unknown period and dispersion measure, you fold all the signals at some speculative period, then shift the frequencies by a speculative dispersion measure and add them together. Now we have a two-dimensional search space to go through. This approach takes a lot of computer time, trying many different time folding periods and dispersion measures, and has been farmed out as part of distributed “home science” computing projects. The pulsar J2007+2722 was the first pulsar to be discovered by a distributed home computing project[4].
But wait – there’s one more complication. The observed period of a pulsar is equal to the emission period if you observe it from a position in space that is not moving relative to the pulsar. If the observer is moving with respect to the pulsar, then the period experiences a Doppler shift. Imagine you are moving away from a pulsar that is pulsing exactly once per second. A first pulse arrives, but in the second that it takes the next pulse to arrive, you have moved further away, so the radio signal has to travel further, and it arrives a fraction of a second more than one second after the previous pulse. The difference is fairly small, but noticeable if you are moving fast enough.
The Earth moves around the sun at an orbital speed of 29.8 km/s. So if it were moving directly away from a pulsar, dividing this by the speed of light, each successive pulse would arrive 0.1 milliseconds later than if the Earth were stationary. This would actually not be a problem, because instead of folding at a period of 1.0000 seconds, we could detect the pulsar by folding at a period of 1.0001 seconds. But the Earth doesn’t move in a straight line – it orbits the sun in an almost circular ellipse. On one side of the orbit the pulsar period is measured to be 1.0001 s, but six months later it appears to be 0.999 s.
This doesn’t sound like much, but if you observe a pulsar for an hour, that’s 3600 seconds, and the cumulative error becomes 0.36 seconds, which is far more than enough to completely ruin your signal, smearing it out so that it becomes undetectable. Hewish and Bell, in their original pulsar detection paper, used the fact that they observed this timing drift consistent with Earth’s orbital velocity to narrow down the direction that the pulsar must lie in (their telescope received signals from a wide-ish area of sky, making pinpointing the direction difficult).
What’s more, not just the orbit of the Earth, but also the rotation of the Earth affects the arrival times of pulses. When a pulsar is overhead, it is 6370 km (the radius of the Earth) closer than when it is on the horizon. Light takes over 20 milliseconds to travel that extra distance – a huge amount to consider when folding pulsar data. So if you observe a pulsar over a single six-hour session, the period can drift by more than 0.02 seconds due to the rotation of the Earth.
These timing drifts can be corrected in a straightforward manner, using the astronomical coordinates of the pulsar, the latitude and longitude of the observatory, and a bit of trigonometry. So in practice these are the steps to detect undiscovered pulsars:
- Observe a patch of sky at multiple radio frequencies for several hours, or even several days, to collect enough data.
- Correct the timing of all the data based on the astronomical coordinates, the latitude and longitude of the observatory, and the rotation and orbit of the Earth. This is a non-linear correction that stretches and compresses different parts of the observation timeline, to make it linear in the pulsar reference frame.
- Perform epoch folding with different values of period and dispersion measure, and look for the emergence of a significant signal above the noise.
- Confirm the result by observing with another observatory and folding at the same period and dispersion measure.
This method has been wildly successful, and as of September 2019 there are 2796 known pulsars[5].
If step 2 above were omitted, then pulsars would not be detected. The timing drifts caused by the Earth’s orbit and rotation would smear the integrated signal out rather than reinforcing it, resulting in it being undetectable. The latitude and longitude of the observatory are needed to ensure the timing correction calculations are done correctly, depending on where on Earth the observatory is located. It goes almost without saying that the astronomers use a spherical Earth model to get these corrections right. If they used a flat Earth model, the method would not work at all, and we would not have detected nearly as many pulsars as we have.
Addendum: Pulsars are dear to my own heart, because I wrote my physics undergraduate honours degree essay on the topic of pulsars, and I spent a summer break before beginning my Ph.D. doing a student project at the Australia Telescope National Facility, taking part in a pulsar detection survey at the Parkes Observatory Radio Telescope, and writing code to perform epoch folding searches.
Some of the data I worked on included observations of pulsar B0540-69, which was first detected in x-rays by the Einstein Observatory in 1984[6], and then at optical wavelengths in 1985[7], flashing with a period of 0.0505697 seconds. I made observations and performed the data processing that led to the first radio detection of this pulsar[8]. (I’m credited as an author on the paper under my unmarried name.) I can personally guarantee you that I used timing corrections based on a spherical model of the Earth, and if the Earth were flat I would not have this publication to my name.
References:
[1] Lyne, A. G., Smith, F. G. Pulsar Astronomy. Cambridge University Press, Cambridge, 1990.
[2] Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., Collins, R. A. “Observation of a Rapidly Pulsating Radio Source”. Nature, 217, p. 709-713, 1968. https://doi.org/10.1038/217709a0
[3] Lorimer, D. R., Kramer, M. Handbook of Pulsar Astronomy. Cambridge University Press, Cambridge, 2012.
[4 Allen, B., Knispel, B., Cordes, J.; et al. “The Einstein@Home Search for Radio Pulsars and PSR J2007+2722 Discovery”. The Astrophysical Journal, 773 (2), p. 91-122, 2013. https://doi.org/10.1088/0004-637X/773/2/91
[5] Hobbs, G., Manchester, R. N., Toomey, L. “ATNF Pulsar Catalogue v1.61”. Australia Telescope National Facility, 2019. https://www.atnf.csiro.au/people/pulsar/psrcat/ (accessed 2019-10-09).
[6] Seward, F. D., Harnden, F. R., Helfand, D. J. “Discovery of a 50 millisecond pulsar in the Large Magellanic Cloud”. The Astrophysical Journal, 287, p. L19-L22, 1984. https://doi.org/10.1086/184388
[7] Middleditch, J., Pennypacker, C. “Optical pulsations in the Large Magellanic Cloud remnant 0540–69.3”. Nature. 313 (6004). p. 659, 1985. https://doi.org/10.1038/313659a0
[8] Manchester, R. N., Mar, D. P., Lyne, A. G., Kaspi, V. M., Johnston, S. “Radio Detection of PSR B0540-69”. The Astrophysical Journal, 403, p. L29-L31, 1993. https://doi.org/10.1086/186714


That’s really cool. 0.05 second per rotation? Correct me if I’m wrong, but isn’t that extremely fast for a pulsar?
By standard pulsar standards, it’s on the quick side, but the millisecond pulsar (MSP) is a different kettle of fish. One example from Wikipedia’s page on pulsars is: J0437-4715 has a period of 0.005757451936712637 s with an error of 1.7×10−17 s, which is ten times faster still (and ludicrously precisely measured).
A lot of the older literature on pulsars was probably set down before we’d gotten a handle on MSPs – bear in mind that for particularly fast pulsars, you’d need equipment that can take measurements quickly enough to resolve the individual pulses. Which means that until such equipment was developed only the slower pulsars would be discovered. That, in turn, would mean our older “lists of known pulsars” were biased in favour of the slower ones, with the faster pulsars being perceived more as celestial tone generators, if they were detected at all.
We’ve got good enough detectors now that most of the MSPs are recognised as such, even though they are thought to be a slightly different kind of entity.
With all that said, Earth’s spherical nature would, of course, still need to be factored into any measurements taken of MSPs.
https://en.wikipedia.org/wiki/Pulsar#cite_note-19
Not really. Brand new pulsars can spin as fast as 1000 Hz, so 0.001 seconds per rotation.
As the above replies say, it’s not especially unusual. Pulsars are typically born with spin rates approximately once per second, but they can be spun up to much faster speeds by accreting matter from a binary companion. The incoming matter adds angular momentum, spinning the neutron star faster and faster. They can get close to 1 millisecond in period before the rotation flings them apart, overcoming the high gravity.
I’m old. I had my limited college astronomy courses in the 1970s. Thanks.
Bah. There’s a perfectly reasonable alternative explanation. The massive elephants upon whose back the Earth lies have to breathe, don’t they? Clearly the Earth rises and falls once daily with the contraction of the elephantine diaphragms (these elephants breathe slowly). The timing corrections used in detecting pulsars work equally well for a rotating spherical Earth as they do for a flat Earth that moves up and down in a sinusoidal wave.
Don’t forget that you also have to factor in the strokes of the Turtle’s flippers as well. It’s a small contribution, but it’s there.
We’re trying to be accurate here, after all.
Mistake in the text: “Collapsing from stellar size down to 10 kilometres produces an increase in rotation period from several days to the incredible rate of about once per second.” Collapsing increases the rotation *rate* but consequently *decreases* the rotation period; and you go from (a period of) “several days” to (a rate of) “once per second”. The result is a mish-mash of rate and period. Either “produces an increase in rotation rate from once in several days to … once per second” or “produces a decrease in rotation period from several days to … about a second”.
Thanks, I’ll fix that!