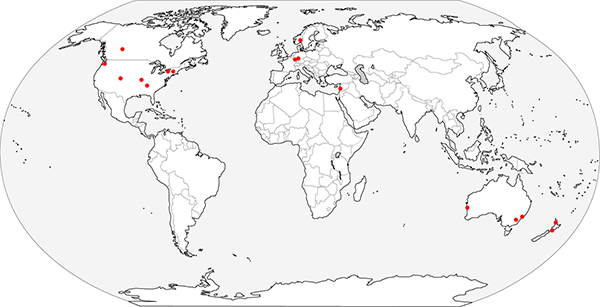
Thank you to everyone who participated in our measurement of the Earth using Eratosthenes’ method! And thank you to those who tried but were frustrated by the weather – I received several reports of bad weather from the UK, France, and parts of the USA. But we have collected 19 successful observations, from 7 countries: New Zealand, Australia, Israel, Germany, Norway, USA, and Canada. I’ve plotted the locations of the observations on the following map.
The reason we did this experiment on the date of the equinox (20/21 March) is because that is when the sun is directly over the equator. Rather than use ancient Syene in Egypt as our reference point, where the sun is directly overhead on the summer solstice, we’re doing our calculations based on distance from the equator.
Ideally, I’d have asked all of you to measure the length of your vertical stick, the length of its shadow, and the distance you are away from the nearest point where your stick cast no shadow (which would be on the equator either due south or north of your location). Although in principle you can measure your distance from this point by travelling due south or north to the equator and keeping an accurate log of distance travelled, this would almost certainly have lowered the participation numbers! So as a proxy, I asked for your locations – either the city, or an accurate reading of your latitude from a GPS unit or Google Maps or something similar. This is really just a shortcut so that I can calculate your distance from the equator. And yes, although the existence of “degrees of latitude” is based on the premise that the Earth is spherical, the simple multiplicative relationship between distance and the numbers we call “latitude” still holds in the real world (even if the Earth is flat).
Some summary statistics:
- Number of data points: 19
- Shortest distance from equator: 3196 km (Geraldton, Australia)
- Longest distance from equator: 6662 km (Oslo, Norway)
- Shortest stick used: 31.5 cm
- Longest stick used: 250.2 cm
The calculations proceeded as follows:
1. For each location, I calculated the distance from the equator, using the provided latitude.
2. I calculated the angle of the stick’s shadow from the vertical: shadow angle = arctangent(shadow length / stick length).
3. I calculated the circumference of the Earth for each measurement: circumference = 4 × distance from equator × 90°/(shadow angle). Here is a graph of the resulting 19 measurements of the Earth’s circumference, plotted against the length of the stick used in each case.
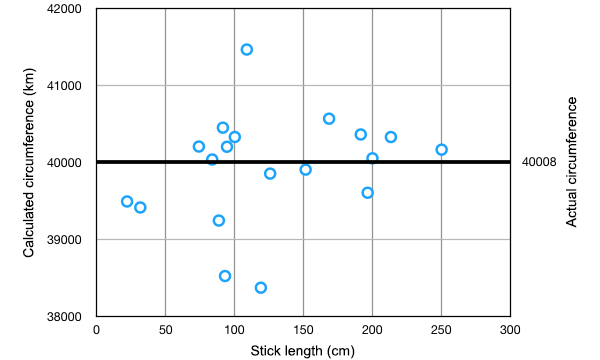
4. I calculated the average of the 19 different measurements of circumference, as well as the standard error of the mean, a statistical measure of the expected uncertainty in the average value. (In experiments like this, where we take multiple independent measurements of the same value, we expect there to be some random errors in each result, caused by slight inaccuracies in measuring the lengths of the sticks and shadows. Our best overall estimate is the average of the results, and the amount of scatter in the results can be used to estimate the likely size of any error in the average.)
The result we achieved is that we measured the circumference of the Earth to be 39926 km, with a standard error of 163 km, or (39926 ± 163) km. What this means is that statistically we expect the true value to lie somewhere between 39763 km and 40089 km.
The polar circumference of the Earth is in fact 40008 km, which lies neatly within this range. So we did it! We measured the circumference of the Earth, and we got the right answer to within the statistical uncertainty of our method!
In one small wrinkle, when everyone was reporting their measurements to me, one person reported that his measurement might be a little bit wrong, because he didn’t have access to a level or any other means of ensuring that his stick was exactly vertical when he took the measurement. So he was unsure whether his data should really be included or not. As it turns out, his data produced the measurement with the largest error, the lowest data point on the graph. If we remove his measurement, our average and standard error become: (40012 ± 147) km. Our average is now even closer to the correct answer, a mere 4 km different. If we made many more measurements, being careful to minimise our random errors, we could expect our result to be even better.
So thank you again to all who participated. Now you can honestly brag that you have measured the size of the Earth!
I can’t speak about how latitudes are defined on any flat earth model, but on the ellipsoidal earth model, latitudes are defined by the orientation of the vertical, and distances to the equator aren’t a simple linear function of the latitude. (Take a look at a very eccentric ellipse to see why this must be so.) This leads into elliptic integrals, but there are some very good approximations that are used in practice, and there are on-line calculators willing to do the work. For mid latitudes, the error with assuming a sphere seems to be about one part in 300.
I’m using Eratosthenes’ assumption that the Earth is a sphere, ignoring the slight ellipticity. If the error is 1 in 300, that’s about 130 km. Maybe I’ll redo the calculations with the more correct figures and see what happens.
I seem to be doing something wrong, because my numbers for the distance from the equator for the two cities you gave differ by thousands of km.
Oh! Yikes… I double checked my calculations and I was the one who was making the mistake. I had some extra trig functions thrown into my calculation. It affected the city-equator distances, but made almost no difference to the final result. I’ve updated the numbers.
Gah, I had my measurements but left them at work, where I have no access to email, and kept forgetting to bring them home. Sorry.
I’m with Lee — can’t recreate the “distance from equator” numbers. Following the surface, the Geraldton number is 50% too high and Oslo 30% (lat/360*40000km). The reported distances are both 57% more than the distance perpendicular to earth-sun line (r*sin); looked like the same ratio.
Notably, the poles are only about 6350 km from the center of the earth and about 10000 km from the equator (if globe). So the 8600 for Oslo (60° north) looks rather strange.
Got it — 57% too high is 1.57 times the actual amount. That is: pi/2.
The “distance from equator” was calculated as circumference * sin(lat), rather than radius * sin(lat).
Yes, that was the problem, but my next step made the same mistake in reverse! I’ve fixed the distance numbers, but you might still be seeing a cached copy of the old numbers.