[audio version of this article]
Meteors are small interplanetary objects that cause visible streaks of light in the sky when they collide with the Earth’s atmosphere. Before this visible collision, the object in space is called a meteoroid, and if any pieces of the object survive to land on the surface of Earth they are called meteorites. Meteoroids are considered to range from roughly the size of a peppercorn up to about a metre across. Larger objects are generally called asteroids, while smaller ones are micrometeoroids or space dust.
Most meteoroids are made of various types of rock, but a small percentage are mostly iron or iron-nickel alloy, and a few are icy. There are vast numbers of these objects in orbit around the sun, and many million enter the Earth’s atmosphere every day, although only a small fraction of those are large enough to produce a meteor trail visible to the human eye. Meteoroids originate from the asteroid belt, or as broken off parts of comets. These small objects are very easily perturbed by the gravity of large objects in the solar system, which effectively randomises their orbits. So in any region of the solar system, the positions and velocities of meteoroids is more or less random.
From an observation point on Earth, we can watch for meteors. Better than counting by eye, we have built specialised radar systems that can detect meteors with greater sensitivity, including during daylight hours, and we can set them up counting meteors all day, every day. Every time the radar detects a meteor, it can record where in the sky it was, what direction it moved, and what time the event occurred. Thinking about the time in particular, we can count how many meteors arrive during any given hour, and average this over many days to produce an hourly rate of meteor events. Many experiments do just this.
Let’s consider what time of day meteors arrive, and if the hourly rate of meteors is the same at all times, or if it varies with time. If the Earth were flat, how might we expect the hourly rate of meteors to behave? Is there any reason to think that the hourly rate of meteors might be different at, say, 8pm, compared to 4am? Or midnight? If the Earth is flat, then… meteors should probably arrive at the same rate all the time. There’s no obvious reason to think it might vary at all.
What happens in reality?
There are several published studies showing measurements of the hourly arrival rate of meteors versus the time of day. Here are some graphs from one such paper (reference [1]):
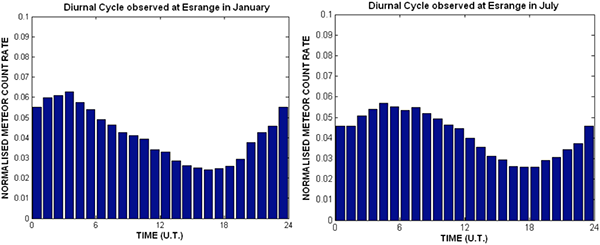
These graphs show the average number of meteors observed arriving during each hour of the day as observed by a meteor-detecting radar station at the Esrange Space Centre near Kiruna in Sweden. The numbers on the vertical axis are normalised so that the 24 hourly bins add up to 1. As shown earlier in the paper, the total number of meteors observed per day is roughly 2000 to 5000, for an overall average of approximately 150 per hour. The times on the horizontal axis are in Universal Time, but Sweden’s time zone is UTC+1, so local midnight occurs at 23 on the graph. Notice that the number of meteors observed per hour is not constant throughout the day, but varies in a systematic pattern. Hmmm.
Here’s another set of data (reference [2]):
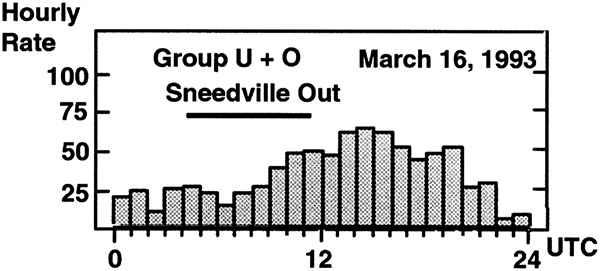
This shows the hourly arrival rate of meteors for a single day as recorded by the American Meteor Society Radiometer Project stations in the southern USA. Again, the times shown are UTC, but the time zone is UTC-6, so local midnight occurs at 6 on the graph.
For good measure, here’s one more (reference [3]):
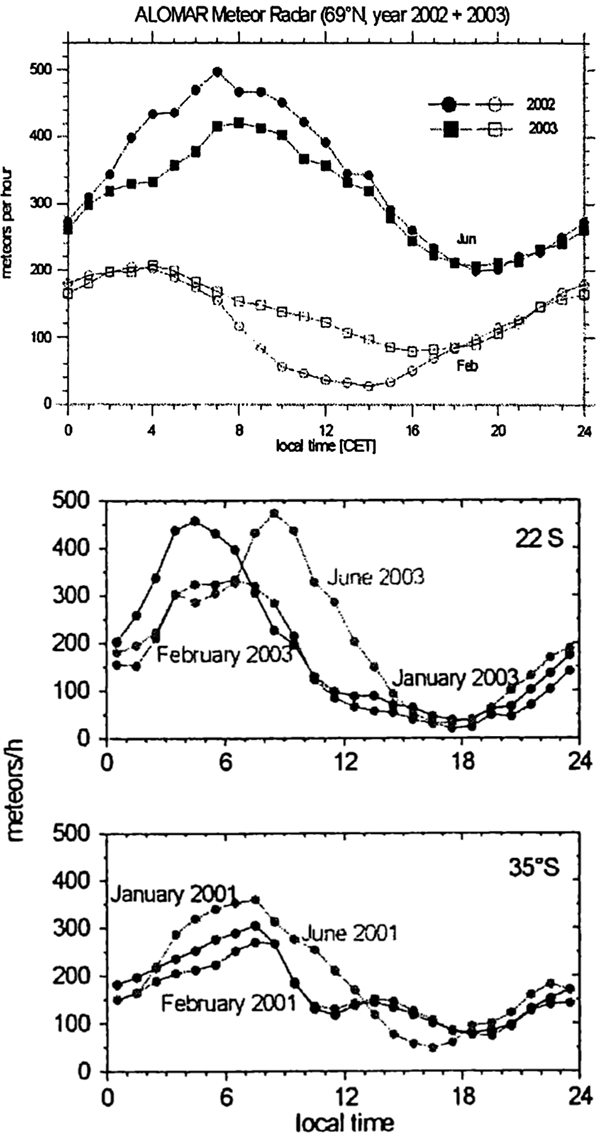
These plots show the hourly arrival rate of meteors at three separate SKiYMET meteor observation sites, at latitudes 69°N, 22°S, and 35°S respectively. The times shown on the horizontal axis here are all local times.
Now, notice how in all of these graphs that the hourly arrival rate of meteors varies by time of day. In particular, in every case there is a maximum in the arrival rate at around 6am local time (to within 2 or 3 hours), and a minimum at around 6pm local time. This pattern, once you notice it, is striking. What could be the cause?
The Earth is moving in its orbit about the sun. In other words, it is sweeping through space, in an almost circular path around the sun. Now, remember that the distribution of meteoroid locations and velocities in space is essentially random. If the Earth is moving through this random scattering of meteoroids, it should sweep up more meteors on the side of the planet that is moving forwards, and fewer on the side that is trailing. And the Earth is also rotating about its axis, this rotation being what causes the daily variation of night and day – in other words the times of the day.

The side of the Earth that is moving forwards is the side where the rotation of the Earth is bringing the dark part of the Earth into the light of the sun, at the dawn of a new day. We call this the dawn terminator. In terms of the clock and time zones, this part of the Earth has a time around 6am. The trailing side of the Earth is the sunset terminator, with a time around 6pm. There will be some variation, up to a couple of hours or so at moderate latitudes, caused by the seasons (the effect of the tilt in the Earth’s rotation axis relative to its orbit).
In other words, if the Earth is a rotating sphere in space, orbiting around the sun, we should expect that the dawn part of the Earth, where the local time is around 6am, should sweep up more meteors than the sunset part of the Earth, where the local time is around 6pm. And if the Earth is a sphere, this variation should be sinusoidal – the distinctive smooth shape of a wave as traced out by points rotating around a circle.
And this is exactly what we see. The variation in the hourly arrival rate of meteors, as observed all across the Earth, matches the prediction you would make if the Earth was a globe. One consequence of the Earth being a globe is that if you want to see meteors – other than during one of the regular annual meteor showers – it’s much better to get up before dawn than to stay up late.
References:
[1] Younger, P. T.; Astin, I.; Sandford, D. J.; and Mitchell, N. J. “The sporadic radiant and distribution of meteors in the atmosphere as observed by VHF radar at Arctic, Antarctic and equatorial latitudes”, Annales Geophysicae, 27, p. 2831-2841, 2009. https://doi.org/10.5194/angeo-27-2831-2009
[2] Meisel, D. D.; Richardson, J. E. “Statistical properties of meteors from a simple, passive forward scatter system”. Planetary and Space Science, 47, p. 107-124, 1999. https://doi.org/10.1016/S0032-0633(98)00096-8
[3] Singer, W; von Zahn, U; Batista, Paulo; Fuller, Brian; and Latteck, Ralph. “Diurnal and annual variations of meteor rates at latitudes between 69°N and 35°S”. In The 17th ESA Symposium on European Rocket and Balloon Programmes and Related Research, Sandefjord, Norway, 2005, ISBN 92-9092-901-4, p. 151-156. https://www.researchgate.net/publication/252769360_Diurnal_and_annual_variations_of_meteor_rates_at_latitudes_between_69N_and_35S

You’ve proven that the Earth rotates and moves through space. This is not a proof that the Earth is a globe. Why couldn’t a flat discworld rotate and orbit?. Why couldn’t it rotate and move through space in a linear manner, while the geocentrist’s tiny sun orbits it? (That latter being close to an actual model some geocentrists use.)
In the spirit of the inspirational pamphlet, I assume several “proofs” will merely be “evidence consistent with the main hypothesis”
In this case, however, the smooth sinosoidal curve implies a smooth transition, and a comparison of data from different longitudes should show smooth transitions consistent with a sphere.
Carl: If the Earth was a flat disc, rotating and orbiting through space, the timing of peak meteors would not be dependent on location of the observer. It would correlated with UTC not Local time.
Also what’s the point of having a flat Earth if it isn’t stationary?
Indeed, if the Sun is tiny, and rotates around the Earth, what then is the Earth rotating around?
I’m not a flat earther, I’m just looking at the argument presented, and I’m with Carl here, there’s nothing actually proving sphere here yet. The facts are consistent with the ‘leading edge of the earth getting more meteorites’, but they don’t seem to imply sphere.
Science doesn’t really “prove” anything in the hard sense of the word of “demonstrating conclusively to the exclusion of all other explanations”. Science comes up with a model (in this case the Earth is spherical), and then accumulates evidence that is consistent with it – or finds an observation that disproves it. What we’re doing here in this blog is accumulating consistent evidence, not supplying a hundred definitive proofs each with no other possible explanation.
Maybe I should write an auxiliary page about the concept of scientific evidence.
I think this particular proof would also hold for a cylindrical earth if it was aligned correctly. You would still get the distinctive sinusoidal wave in the meteor arrival times.
With the data shown only on this page maybe, but don’t forget that the Earth’s axis is tilted. I suspect that at the poles you’d get a similar sinusoidal pattern–except it would map out over a one-year period instead of a one-day period since each pole spends half the year pointing away from the direction of Earth’s movement along its orbit.
It might also hold (in a rough way) for other “roundish” shapes like a rhombicosidodecahedron as well… but I see the main point of this blog as differentiating between the round (or spherical – or indeed roughly spherical) model and the flat model (which is supported as a credible contender – rightly or wrongly – by bodies of literature and a league of surprisingly vocal advocates).
Very good observation, though…!
The last time I visited the American Museum of Natural History in NY, NY, the exhibit that wowed me the most was a meteorite section on display. A similar section is shown in the wikipedia entry
https://en.wikipedia.org/wiki/Meteorite
with the caption
“A cut and polished slice of the Esquel meteorite, a stony-iron pallasite. Yellow-green olivine crystals are encased in the iron-nickel matrix.”
This is not the same one I saw, and a picture truly fails to do it justice anyway. The meteorite was presumed to be from the transition region from mantle to core of a large body that broke up in an ancient collision. It’s a slab of iron, with large (thumb-sized) olivine crystals embedded in it. The way the light passes through the crystals is amazingly beautiful, but it is the knowledge that this is just what we have on the edge of the earth’s core, thousands of miles beneath our feet, that totally wowed me.
Incredible.
While the evidence here is sufficient to show a spherical earth. The argument falls short by a crucial step. the sinusoidal pattern is consistent with a rotation, but DOESN’T require a sphere. A plane would show the same pattern. You need to show globally correlated offsets in the sine wave (offset relative to global time not local) to prove a sphere. In fact the data was presented! (the second point was the US observations) But the argument was not made.
“any many” should be “and many”.
Fixed, thanks!