Following the rediscovery of the New World by Europeans in the 15th century, the great seafaring nations of Europe rapidly mapped the eastern coastlines of the Americas. Demand for maps grew, not just of the New World, but of the Old as well. This made it possible for a young man (unfortunately women were shepherded into more domestic jobs) to seek his fortune as a mapmaker. One such man was Abraham Ortelius, who lived in Antwerp in the Duchy of Brabant (now part of Belgium).

Abraham Ortelius, painted by Peter Paul Rubens. (
Public domain image from Wikimedia Commons.)
In 1547, at the age of 20, Ortelius began his career as a map engraver and illuminator. He travelled widely across Europe, and met cartographer and mapmaker Gerardus Mercator (15 years his senior, and whose map projection we met in 14. Map projections) in 1554. The two became friends and travelled together, reinforcing Ortelius’s passion for cartography, as well as the technical and scientific aspects of geography. Ortelius went on to produce and publish several maps of his own, culminating in his 1570 publication, Theatrum Orbis Terrarum (“Theatre of the Orb of the World”), now regarded as the first modern atlas of the world (as then known). Previously maps had been sold as individual sheets or bespoke sets customised to specific needs, but this was a curated collection intended to cover the entire known world in a consistent style. The Theatrum was wildly successful, running to 25 editions in seven languages by the time of Ortelius’s death in 1598.
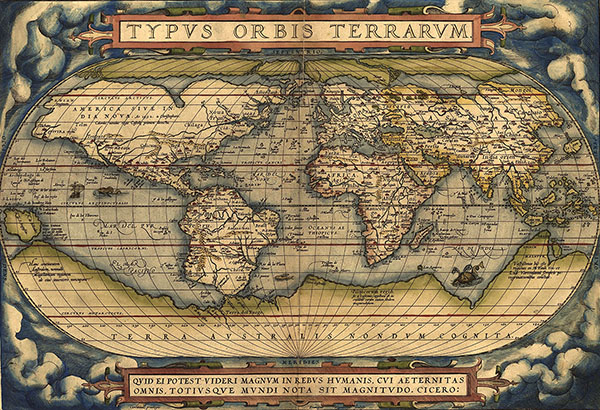
World map plate from
Theatrum Orbis Terrarum. (
Public domain image from Wikimedia Commons.)
Being intimately familiar with his maps, Ortelius noticed a strange coincidence. In his publication Thesaurus Geographicus (“Geographical Treasury”) he wrote about the resemblance of the shapes of the east coast of the Americas to the west coasts of Europe and Africa across the Atlantic Ocean. He suggested that the Americas may have been “torn away from Europe and Africa … by earthquakes and floods. … The vestiges of the rupture reveal themselves, if someone brings forward a map of the world and considers carefully the coasts of the three.” This is the first known suggestion that the uncanny jigsaw-puzzle appearance of these coastlines might not be a coincidence, but rather a vestige of the continents actually having fitted together in the past.
Ortelius wasn’t the only one to make this observation and reach the same conclusion. Over the next few centuries, similar thoughts were proposed by geographers Theodor Christoph Lilienthal, Alexander von Humboldt, Antonio Snider-Pellegrini, Franklin Coxworthy, Roberto Mantovani, William Henry Pickering, Frank Bursley Taylor, and Eduard Suess. Suess even suggested (in 1885) that at some time in the past all of the Earth’s continents were joined in a single mass, which he gave the name “Gondwana”.
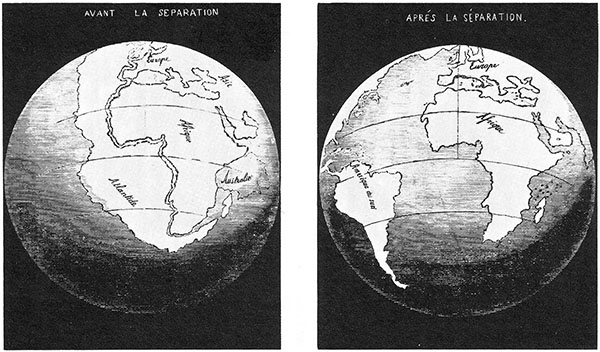
Illustration by Antonio Snider-Pellegrini, of his proposal that the Americas had once been adjacent to Europe and Africa. (
Public domain image from Wikimedia Commons.)
Although many people had suggested that the continents had once been adjacent, nobody had produced any supporting evidence, nor any believable mechanism for how the continents could move. This changed in 1912, when the German meteorologist and polar scientist Alfred Wegener proposed the theory which he named continental drift. He began with the same observation of the jigsaw nature of the continent shapes, but then he applied the scientific method: he tested his hypothesis. He looked at the geology of coastal regions, examining the types of rocks, the geological structures, and the types of fossils found in places around the world. What he found were remarkable similarities in all of these features on opposite sides of the Atlantic Ocean, and in other locations around the world where he supposed that now-separate landmasses had once been in contact. This is exactly what you would expect to find if a long time ago the continents had been adjacent: plants and animals would have a range spanning across what would later split open and become an ocean, and geological features would be consistent across the divide as well[1].
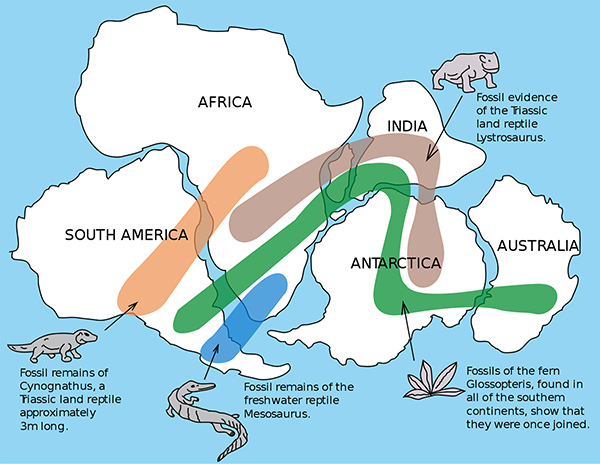
Map of similar fossils of non-sea-going lifeforms found across landmasses, providing evidence that they were once joined. (
Public domain image from Wikimedia Commons.)
In short, Wegener found and presented evidence in support of his hypothesis. He presented his theory, with the evidence he had gathered, in his 1915 book, Die Entstehung der Kontinente und Ozeane (“The Emergence of the Continents and Oceans”). He too proposed that all of the Earth’s continents were at one stage joined into a single landmass, which he named Pangaea (Greek for “all Earth”)[2].
But Wegener had two problems. Firstly, he still didn’t know how continents could possibly move. Secondly, he wasn’t a geologist, and so the establishment of geologists didn’t take him very seriously, to say the least. But as technology advanced, detailed measurements of the sea floor were made beginning in the late 1940s, including the structures, rock types, and importantly the magnetic properties of the rocks. Everything that mid-20th century geologists found was consistent with the existence of a large crack running down the middle of the Atlantic Ocean, where new rock material was welling up from beneath the ocean floor, and spreading outwards. They also found areas where the Earth’s crust was being squashed together, and either being thrust upwards like wrinkles in a tablecloth (such as the Himalayas mountain range), or plunged below the surface (such as along the west coast of the Americas).
Confronted with overwhelming evidence—which it should be pointed out was both consistent with many other observations, and also explained phenomena such as earthquakes and volcanoes better than older theories—the geological consensus quickly turned around[3]. The newly formulated theory of plate tectonics was as unstoppable as continental drift itself, and revolutionised our understanding of geology in the same way that evolution did for biology. Suddenly everything made sense.
The Earth, we now know, has a relatively thin, solid crust of rocks making up the continents and sea floors. Underneath this thin layer is a thick layer known as the mantle. The uppermost region of the mantle is solid and together with the crust forms what is known as the lithosphere. Below this region, most of the mantle is hot enough that the material there is visco-elastic, meaning it behaves like a thick goopy fluid, deforming and flowing under pressure. This viscous region of the mantle is known as the asthenosphere.
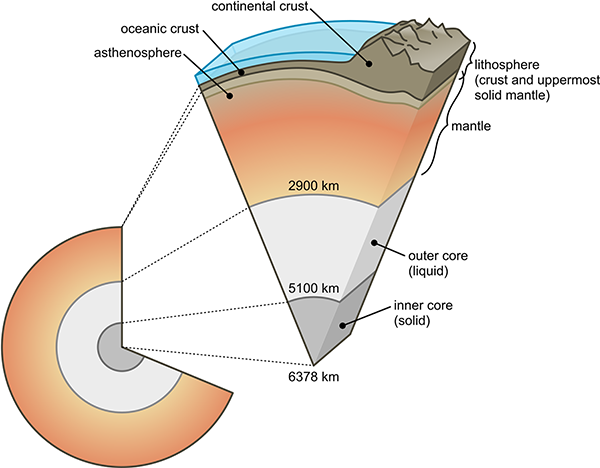
Diagram of the Earth’s layers. The lithosphere region is not to scale and would appear much thinner if drawn to scale. (
Public domain image from Wikimedia Commons.)
Heat wells up from the more central regions of the Earth (generated by radioactive decay). Just like a boiling pot of water, this sets up convection currents in the asthenosphere, where the hot material flows upward, then sideways, then back down to form a loop. The sideways motion at the top of these convection cells is what carries the crust above, moving it slowly across the surface of the planet.
The Earth’s crust is broken into pieces, called tectonic plates, which fit together along their edges. Each plate is relatively rigid, but moves relative to the other plates. Plates move apart where the upwelling of the convection cells occurs, such as along the Mid-Atlantic Ridge (the previously mentioned crack in the Atlantic Ocean floor), and collide and subduct back down along other edges. At some plate boundaries the plates slide horizontally past one another. All of this motion causes earthquakes and volcanoes, which are mostly concentrated along the plate boundaries. The motion of the plates is slow, around 10-100 millimetres a year. This is too slow to notice over human history, except with high-tech equipment. GPS navigation and laser ranging systems can directly measure the movements of the continents relative to one another, confirming the speed of the motion.
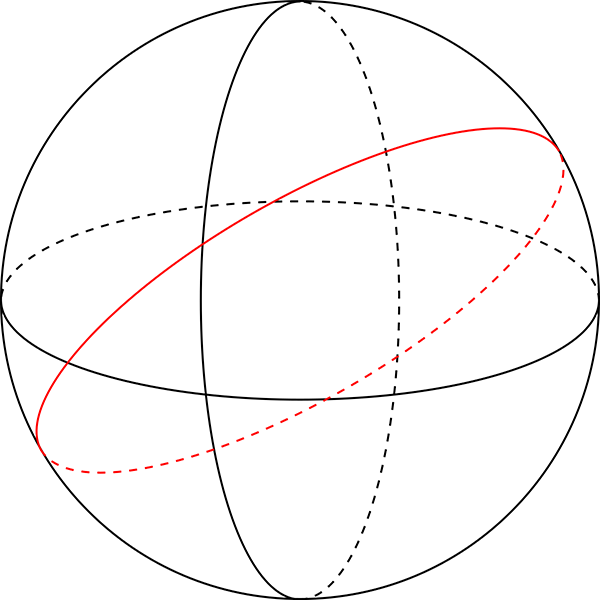
The tectonic plates, then, are shell-like pieces of crust that fit together to form the spherical shape of the Earth’s surface. An equal amount of area is lost at subduction zones as is gained by spreading on sea-floors and in places such as Africa’s Rift Valley, keeping the Earth’s surface area constant. As the plates drift around, they don’t change in size or deform geometrically very much.
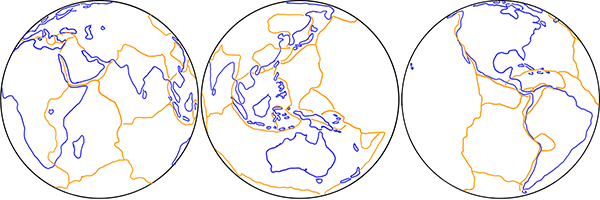
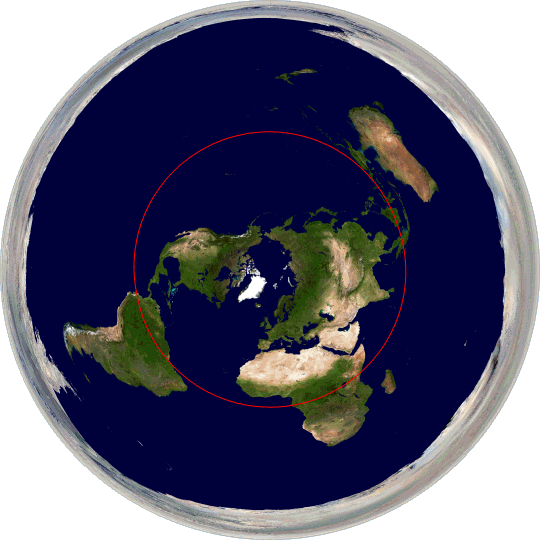
Sketch of the major tectonic plates as they fit together to form the surface of the Earth.
All of this is consistent and supported by many independent pieces of evidence. Direct measurement shows that the continents are moving, so it’s really just a matter of explaining how. But the motions of the tectonic pates only make sense on a globe.
If the Earth were flat, then sure, you could conceivably have some sort of underlying structure that supports the same sort of convection cells and geological processes of spreading and subduction, leading to earthquakes and volcanoes, and so on. But look at the shapes of the tectonic plates.
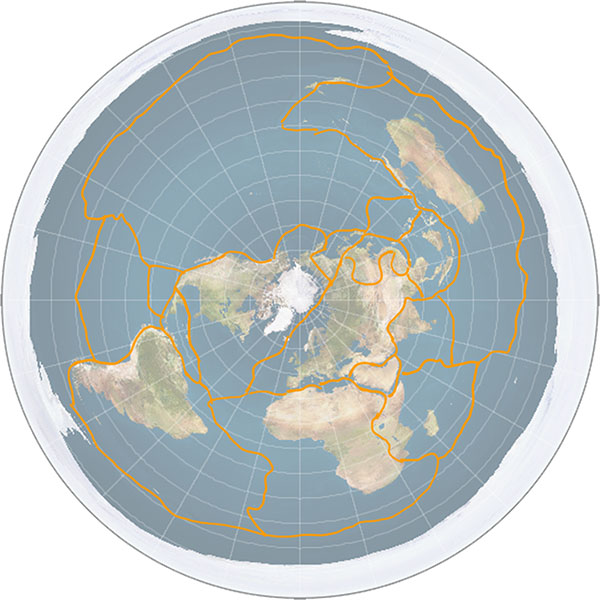
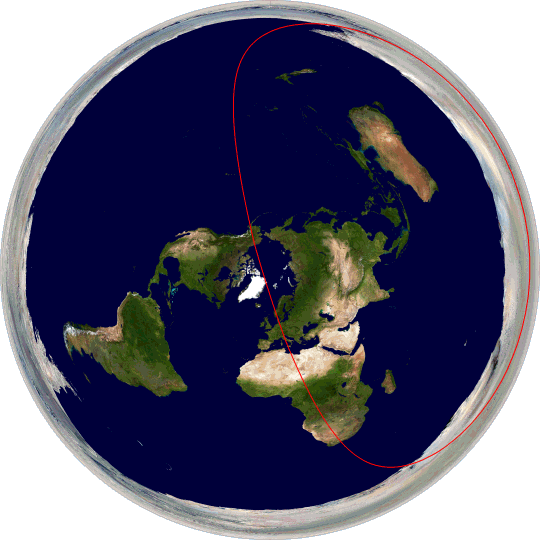
Sketch of the major tectonic plates on a flat Earth.
Because of the distortions in the shape of the map relative to a globe, the tectonic plates need to change shape and size as they move across the surface. Not only that, but consider the Antarctic plate, which is a perfectly normal plate on the globe. On the typical Flat Earth model where Antarctica is a barrier of ice around the edge of the circle, the Antarctic plate is a ring. And when it moves, it not only has to deform in shape, but crust has to disappear off one side of the disc and appear on the other side.
So plate tectonics, the single most fundamental and important discovery in the entire field of geology, only makes sense because the Earth is a globe.
Notes:
[1] For readers interested in this particular aspect of continental drift, I’ve previously written about it at greater length in the annotation to this Irregular Webcomic! http://www.irregularwebcomic.net/1946.html
[2] Pangaea is now the accepted scientific term for the unified landmass when all the continents were joined. Eduard Suess’s Gondwana lives on as the name now used to refer to the conjoined southern continents before merging with the northern ones to form Pangaea.
[3] Alfred Wegener is often cited by various people in support of the idea that established science often laughs at revolutionary ideas proposed by outsiders, only for the outsider to later be vindicated. Often by people proposing outlandish or fringe science theories that defy not only scientific consensus but also the boundaries of logic and reason. What they fail to point out is that in all the history of science, Wegener is almost the only such case, whereas almost every other outsider proposing a radical theory is shown to be wrong. As Carl Sagan so eloquently put it in Broca’s Brain:
The fact that some geniuses were laughed at does not imply that all who are laughed at are geniuses. They laughed at Columbus, they laughed at Fulton, they laughed at the Wright brothers. But they also laughed at Bozo the Clown.