With my Science Club class of 7-10 year olds, I did an experiment to test what factors influence the period of swing of a pendulum, and to measure the strength of Earth’s gravity. I borrowed some brass weights and a retort stand from my old university Physics Department and took them to the school. Then with the children we did the experiment!
We set up pendulums with different lengths of string, measuring the length of each one. With each pendulum length, we tested different numbers of brass weights, and pulling the weight back by a different distance so that the pendulum swung through shorter or longer arcs. For each combination of string length, mass, and swing length, I got the kids to time a total of 10 back and forth swings with a stopwatch. I recorded the times and divided by 10 to get an average swing time for each pendulum.
Here’s a graph showing the pendulum period (or “swing time” as I’m calling it with the kids), plotted against the mass of the weight at the end.
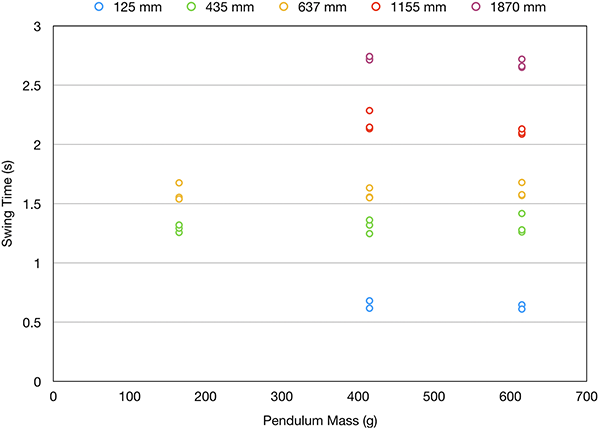
Here’s a graph showing the pendulum period (or “swing time” as I’m calling it with the kids), plotted against the swing distance (i.e. the amplitude).
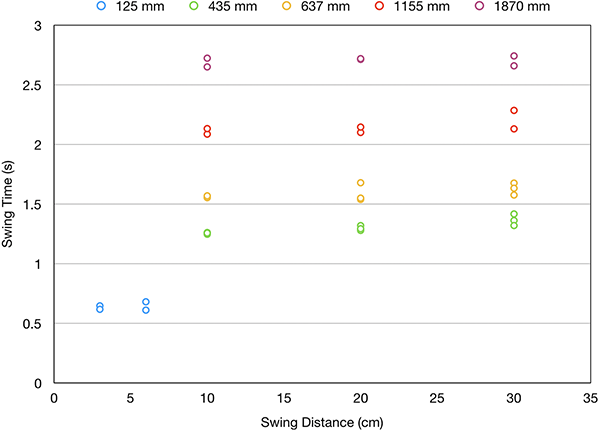
These first two graphs show pretty clearly that the period of the pendulum is not dictated by either the mass of the pendulum or the amplitude of the swing. If you look at the different colours showing the pendulum length, however, you may discern a pattern.
And here’s a graph showing the pendulum period plotted against the length of the pendulum.
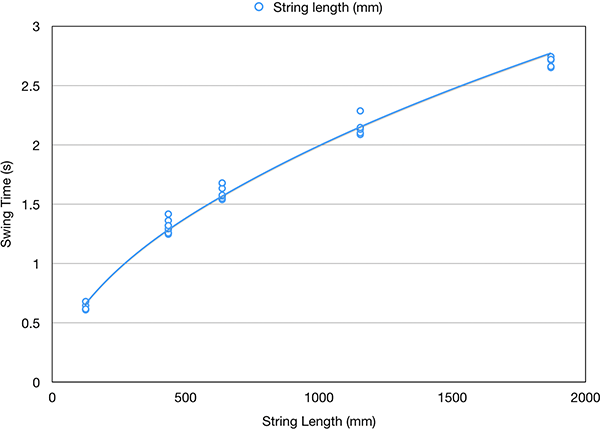
In this case, all the points from different pendulum masses and swing amplitudes but the same length are clustered together (with some scatter caused by experimental errors in using the stopwatch). This indicates that only the length is important in determining the period. This matches the first order approximation theoretical formula for the period of a pendulum, T:
T = 2π√(l/g),
where l is the length and g is the acceleration due to gravity. To calculate g from the experimental data, I squared the period numbers and calculated the slope of the best fit line passing through zero to (i, T2). Then g = 4π2 divided by the slope… which gives g = 10.0 m/s2.
The true value is 9.81 m/s2, so we got it right to a little better than 2%. Which I consider pretty good given the fact that I had kids as young as 7 making the measurements!
Although this is an “other science” entry on this blog and not a proof of the Earth’s roundness, I’m planning to combine the results of this experiment with our ongoing measurement of the sun’s shadow length of a vertical stick at the end of the year, to calculate not only the size of the Earth, but also its mass. It’ll be interesting to see how close we can get to that!
> Although this is an “other science” entry on this blog and not a proof of the Earth’s roundness,
Foucault’s pendulum, though, is at least a proof that The Earth spins.
Which a flat Earth could do; but then the existence of two poles – points that stay still in the sky, as seen by folks far from the equator – (rather than one) presents problems. Furthermore, on a flat Earth, the pendulum would turn once per day, in the same sense, everywhere – rather than rotating -sin(latitude) turns per day; i.e. not rotating at the equator and rotating in opposite directions to the North and South of it.
Moreover, once you get a flat Earth believer to accept that the earth spins, the rest falls apart.
The fixed stars go from being holes in rotating firmament (don’t ask about the southern hemisphere) to fixed things, above the spinning Earth. Now the Sun gets that same spin motion, and just moves a bit to make up other motions it has (seasons etc.) and the moon similar. Everything slows way down. Planets go from spinning around the Earth every day, but coming back to *almost* the same spot at the same time every night, slowly over the years changing that return spot; to just moving a bit every night.