photography – 100 Proofs that the Earth is a Globe

28. Stereo imaging

We see the world in 3D. What this means is that our visual system—comprising the eyes, optic nerves, and brain—takes the sensory input from our eyes and interprets it in a way that gives us the sensation that we exist in a three-dimensional world. This sensation is often called depth perception.

In practical terms, depth perception means that we are good at estimating the relative distances from ourselves to objects in our field of vision. You can tell if an object is nearer or further away just by looking at it (weird cases like optical illusions aside). A corollary of this is that you can tell the three-dimensional shape of an object just by looking at it (again, optical illusions aside). A basketball looks like a sphere, not like a flat circle. You can tell if a surface that you see is curved or flat.

To do this, our brain relies on various elements of visual data known as depth cues. The best known depth cue is stereopsis, which is interpreting the different views of left and right eyes caused by the parallax effect, your brain innately using this information to triangulate distances. You can easily observe parallax by looking at something in the distance, holding up a finger at arms length, and alternately closing left and right eyes. In the view from each eye, your finger appears to move left/right relative to the background. And with both eyes open, if you focus on the background, you see two images of your finger. This tells your brain that your finger is much closer than the background.

Parallax effect

Illustration of parallax. The dog is closer than the background scene. Sightlines from your left and right eyes passing through the dog project to different areas of the background. So the view seen by your left and right eyes show the dog in different positions relative to the background. (The effect is exaggerated here for clarity.)

We’ll discuss stereopsis in more detail below, but first it’s interesting to know that stereopsis is not the only depth cue our brains use. There are many physically different depth cues, and most of them work even with a single eye.

Cover one eye and look at the objects nearby, such as on your desk. Reach out and try to touch them gently with a fingertip, as a test for how well you can judge their depth. For objects within an easy hand’s reach you can probably do pretty well; for objects you need to stretch to touch you might do a little worse, but possibly not as bad as you thought you might. The one eye that you have looking at nearby things needs to adjust the focus of its lens in order to keep the image focused on the retina. Muscles in your eye squeeze the lens to change its shape, thus adjusting the focus. Nerves send these muscle signals to your brain, which subconsciously uses them to help gauge distance to the object. This depth cue is known as accommodation, and is most accurate within a metre or two, because it is within this range that the greatest lens adjustments need to be made.

With one eye covered, look at objects further away, such as across the room. You can tell that some objects are closer and other objects further away (although you may have trouble judging the distances as accurately as if you used both eyes). Various cues are used to do this, including:

Perspective: Many objects in our lives have straight edges, and we use the convergence of straight lines in visual perspective to help judge distances.

Relative sizes: Objects that look smaller are (usually) further away. This is more reliable if we know from experience that certain objects are the same size in reality.

Occultation: Objects partially hidden behind other objects are further away. It seems obvious, but it’s certainly a cue that our brain uses to decide which object is nearer and which further away.

Texture: The texture on an object is more easily discernible when it is nearer.

Light and shadow: The interplay of light direction and the shading of surfaces provides cues. A featureless sphere such as a cue ball still looks like a sphere rather than a flat disc because of the gradual change in shading across the surface.

Shaded circle

A circle shaded to present the illusion that it is a sphere, using light and shadow as depth cues. If you squint your eyes so your screen becomes a bit fuzzy, the illusion of three dimensionality can become even stronger.

Motion parallax: With one eye covered, look at an object 2 or 3 metres away. You have some perception of its distance and shape from the above-mentioned cues, but not as much as if both your eyes were open. Now move your head from side to side. The addition of motion produces parallax effects as your eye moves and your brain integrates that information into its mental model of what you are seeing, which improves the depth perception. Pigeons, chickens, and some other birds have limited binocular vision due to their eyes being on the sides of their heads, and they use motion parallax to judge distances, which is why they bob their heads around so much.

Demonstration of motion parallax. You get a strong sense of depth in this animation, even though it is presented on your flat computer screen. (Creative Commons Attribution 3.0 Unported image by Nathaniel Domek, from Wikimedia Commons.)

There are some other depth cues that work with a single eye as well – I don’t want to try to be exhaustive here.

If you uncover both eyes and look at the world around you, your sense of three dimensionality becomes stronger. Now instead of needing motion parallax, you get parallax effects simply by looking with two eyes in different positions. Stereopsis is one of the most powerful depth cues we have, and it can often be used to override or trick the other cues, giving us a sense of three-dimensionality where none exists. This is the principle behind 3D movies, as well as 3D images printed on flat paper or displayed on a flat screen. The trick is to have one eye see one image, and the other eye see a slightly different image of the same scene, from an appropriate parallax viewpoint.

In modern 3D movies this is accomplished by projecting two images onto the screen simultaneously through two different polarising filters, with the planes of polarisation oriented at 90° to one another. The glasses we wear contain matched polarising filters: the left eye filter blocks the right eye projection while letting the left eye projection through, and vice versa for the right eye. The result is that we see two different images, one with each eye, and our brains combine them to produce the sensation of depth.

Another important binocular depth cue is convergence. To look at an object nearby, your eyes have to point inwards so they are both focused on the same point. For an object further away, your eyes look more parallel. Like your lenses, the muscles that control this send signals to your brain, which it interprets as a distance measure. Convergence can be a problem with 3D movies and images if the image creator is not careful. Although stereopsis can provide the illusion of depth, if it’s not also matched with convergence then there can be conflicting depth cues to your brain. Another factor is that accommodation tells you that all objects are at the distance of the display screen. The resulting disconnects between depth cues are what makes some people feel nauseated or headachy when viewing 3D images.

To create 3D images using stereopsis, you need to have two images of the same scene, as seen from different positions. One method is to have two cameras side by side. This can be used for video too, and is the method used for live 3D broadcasts, such as sports. Interestingly, however, this is not the most common method of making 3D movies.

A 3D camera produced by the Coronet Camera Company. Note the two lenses at the front, separated by roughly the same spacing as human eyes. (Creative Commons Attribution 3.0 Unported image by Wikimedia Commons user Bilby, from Wikimedia Commons.)

3D movies are generally shot with a single camera, and then an artificial second image is made for each frame during the post-production phase. This is done by a skilled 3D artist, using software to model the depths to various objects in each shot, and then manipulate the pixels of the image by shifting them left or right by different amounts, and painting in any areas where pixel shifts leave blank pixels behind. The reason it’s done this way is that this gives the artist control over how extreme the stereo depth effect is, and this can be manipulated to make objects appear closer or further away than they were during shooting. It’s also necessary to match depth disparities of salient objects between scenes on either side of a scene cut, to avoid the jarring effect of the main character or other objects suddenly popping backwards and forwards across scene cuts. Finally, the depth disparity pixel shifts required for cinema projection are different to the ones required for home video on a TV screen, because of the different viewing geometries. So a high quality 3D Blu-ray of a movie will have different depth disparities to the cinematic release. Essentially, construction of the “second eye” image is a complex artistic and technical consideration of modern film making, which cannot simply be left to chance by shooting with two cameras at once. See “Nonlinear disparity mapping for stereoscopic 3D” by Lang et al.[1], for example, which discusses these issues in detail.

For a still photo however, shooting with two cameras at the same time is the best method. And for scientific shape measurement using stereographic imaging, two cameras taking real images is necessary. One application of this is satellite terrain mapping.

The French space agency CNES launched the SPOT 1 satellite in 1986 into a sun-synchronous polar orbit, meaning it orbits around the poles and maintains a constant angle to the sun, as the Earth rotates beneath it. This brought any point on the surface into the imaging field below the satellite every 26 days. SPOT 1 took multiple photos of areas of Earth in different orbital passes, from different locations in space. These images could then be analysed to match features and triangulate the distances to points on the terrain, essentially forming a stereoscopic image of the Earth’s surface. This reveals the height of topographic features: hills, mountains, and so on. SPOT 1 was the first satellite to produce directly imaged stereo altitude data for the Earth. It was later joined and replaced by SPOT 2 through 7, as well as similar imaging satellites launched by other countries.

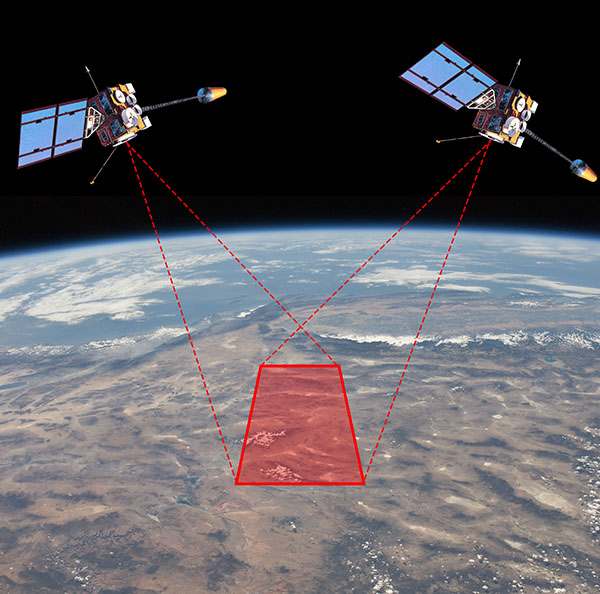
Diagram of satellite stereo imaging

Diagram illustrating the principle of satellite stereo terrain mapping. As the satellite orbits Earth, it takes photos of the same region of Earth from different positions. These are then triangulated to give altitude data for the terrain. (Background image is a public domain photo from the International Space Station by NASA. Satellite diagram is a public domain image of GOES-8 satellite by U.S. National Oceanic and Atmospheric Administration.)

Now, if we’re taking photos of the Earth and using them to calculate altitude data, how important is the fact that the Earth is spherical? If you look at a small area, say a few city blocks, the curvature of the Earth is not readily apparent and you can treat the underlying terrain as flat, with modifications by strictly local topography, without significant error. But as you image larger areas, getting up to hundreds of kilometres, the 3D shape revealed by the stereo imaging consists of the local topography superimposed on a spherical surface, not on a flat plane. If you don’t account for the spherical baseline, you end up with progressively larger altitude errors as your imaged area increases.

A research paper on the mathematics of registering stereo satellite images to obtain altitude data includes the following passage[2]:

Correction of Earth Curvature

If the 3D-GK coordinate system X, Y, Z and the local Cartesian coordinate system X_g, Y_g, Z_g are both set with their origins at the scene centre, the difference in X_g and X or Y_g and Y will be negligible, but for Z and Z_g [i.e. the height coordinates] the difference will be appreciable as a result of Earth curvature. The height error at a ground point S km away from the origin is given by the well-known expression:

ΔZ = Y²/2R km

Where R = 6367 km. This effect amounts to 67 m in the margin of the SPOT scene used for the reported experiments.

The size of the test scene was 50×60 km, and at this scale you get altitude errors of up to 67 metres if you assume the Earth is flat, which is a large error!

Another paper compares the mathematical solution of stereo satellite altitude data to that of aerial photography (from a plane)[3]:

Some of the approximations used for handling usual aerial photos are not acceptable for space images. The mathematical model is based on an orthogonal coordinate system and perspective image geometry. […] In the case of direct use of the national net coordinates, the effect of the earth curvature is respected by a correction of the image coordinates and the effect of the map projection is neglected. This will lead to [unacceptable] remaining errors for space images. […] The influence of the earth curvature correction is negligible for aerial photos because of the smaller flying height Z_f. For a [satellite] flying height of 300 km we do have a scale error of the ground height of 1:20 or 5%.

So the terrain mappers using stereo satellite data need to be aware of and correct for the curvature of the Earth to get their data to come out accurately.

Terrain mapping is done on relatively small patches of Earth. But we’ve already seen in our first proof photos of Earth taken from far enough away that you can see (one side of) the whole planet, such as the Blue Marble photo. Can we do one better, and look at two photos of the Earth taken from different positions at the same time? Yes, we can!

The U.S. National Oceanic and Atmospheric Administration operates the Geostationary Operational Environmental Satellite (GOES) system, manufactured and launched by NASA. Since 1975, NASA has launched 17 GOES satellites, the last four of which are currently operational as Earth observation platforms. The GOES satellites are in geostationary orbit 35790 km above the equator, positioned over the Americas. GOES-16 is also known as GOES-East, providing coverage of the eastern USA, while GOES-17 is known as GOES-West, providing coverage of the western USA. This means that these two satellites can take images of Earth at the same time from two slightly different positions (“slightly” here means a few thousand kilometres).

This means we can get stereo views of the whole Earth. We could in principle use this to calculate the shape of the Earth by triangulation using some mathematics, but there’s an even cooler thing we can do. If we view a GOES-16 image with our right eye, while viewing a GOES-17 image taken at the same time with our left eye, we can get a 3D view of the Earth from space. Let’s try it!

The following images show cross-eyed and parallel viewing pairs for GOES-16/GOES-17 images. Depending on your ability to deal with these images, you should be able to view a stereo 3D image of Earth. (Cross-eyed stereo viewing seems to be the most popular method on the Internet, but personally I’ve never been able to get it to work for me, whereas I find the parallel method fairly easy. I find it works best if I put my face very close to the screen to lock onto the initial image fusion, and then slowly pull my head backwards. Another option if you have a VR viewer for your phone, like Google Cardboard, is to load the parallel image onto your phone and view it with your VR viewer.)

GOES stereo image, cross-eyed

Stereo pair images of Earth from NASA’s GOES-16 (left) and GOES-17 (right) satellites taken at the same time on the same date, 1400 UTC, 12 July 2018. This is a cross-eyed viewing pair: to see the 3D image, cross your eyes until three images appear, and focus on the middle image. It will probably be easier if you reduce the size of the image on your screen using your browser’s zoom function. (Public domain image by NASA, from [4].)

GOES stereo image, parallel

The same stereo pair presented with GOES-16 view on the right and GOES-17 on the left. This is a parallel viewing pair: to see the 3D image relax your eyes so the left eye views the left image and the right eye views the right image, until three images appear, and focus on the middle image. It will probably be easier if you reduce the size of the image on your screen using your browser’s zoom function. (Public domain image by NASA, from [4].)

Unfortunately these images are cropped, but if you managed to get the 3D viewing to work, you will have seen that your brain automatically does the distance calculation ting as it would with a real object, and you can see for yourself with your own eyes that the Earth is rounded, not flat.

I’ve saved the best for last. The Japan Meteorological Agency operates the Himawari-8 weather satellite, and the Korea Meteorological Administration operates the GEO-KOMPSAT-2A satellite. Again these are both on geosynchronous orbits above the equator, this time placed so that Himawari-8 has the best view of Japan, while GEO-KOMPSAT-2A has the best view of Korea, situated slightly to the west. And here I found uncropped whole Earth images from these two satellites taken at the same time, presented again as cross-eyed and then parallel viewing pairs:

Himawari-KOMPSAT stereo image, cross-eyed

Stereo pair images of Earth from Japan Meteorological Agency’s Himawari-8 (left) and Korea Meteorological Administration’s GEO-KOMPSAT-2A (right) satellites taken at the same time on the same date, 0310 UTC, 26 January 2019. This is a cross-eyed viewing pair. (Image reproduced and modified from [5].)

Himawari-KOMPSAT stereo image, parallel

The same stereo pair presented with Himawari-8 view on the right and GEO-KOMPSAT-2A on the left. This is a parallel viewing pair. (Image reproduced and modified from [5].)

For those who have trouble with free stereo viewing, I’ve also turned these photos into a red-cyan anaglyphic 3D image, which is viewable with red-cyan 3D glasses (the most common sort of coloured 3D glasses)

Himawari-KOMPSAT stereo image, anaglyph

The same stereo pair rendered as a red-cyan anaglyph. The stereo separation of the viewpoints is rather large, so it may be difficult to see the 3D effect at full size – it should help to reduce the image size using your browser’s zoom function, place your head close to your screen, and gently move side to side until the image fuses, then pull back slowly.

Hopefully you managed to get at least one of these 3D images to work for you (unfortunately some people find viewing stereo 3D images difficult). If you did, well, I don’t need to point out what you saw. The Earth is clearly, as seen with your own eyes, shaped like a sphere, not a flat disc.

References:

[1] Lang, M., Hornung, A., Wang, O., Poulakos, S., Smolic, A., Gross, M. “Nonlinear disparity mapping for stereoscopic 3D”. ACM Transactions on Graphics, 29 (4), p. 75-84. ACM, 2010. http://dx.doi.org/10.1145/1833349.1778812

[2] Hattori, S., Ono, T., Fraser, C., Hasegawa, H. “Orientation of high-resolution satellite images based on affine projection”. International Archives of Photogrammetry and Remote Sensing, 33(B3/1; PART 3) p. 359-366, 2000. https://www.isprs.org/proceedings/Xxxiii/congress/part3/359_XXXIII-part3.pdf

[3] Jacobsen, K. “Geometric aspects of high resolution satellite sensors for mapping”. ASPRS The Imaging & Geospatial Information Society Annual Convention 1997 Seattle. 1100(305), p. 230, 1997. https://www.ipi.uni-hannover.de/uploads/tx_tkpublikationen/jac_97_geom_hrss.pdf

[4] CIMSS Satellite blog, Space Science and Engineering Center, University of Wisconsin-Madison, “Stereoscopic views of Convection using GOES-16 and GOES-17”. 2018-07-12. https://cimss.ssec.wisc.edu/goes/blog/archives/28920 (accessed 2019-09-26).

[5] CIMSS Satellite blog, Space Science and Engineering Center, University of Wisconsin-Madison, “First GEOKOMPSAT-2A imagery (in stereo view with Himawari-8)”. 2019-02-04. https://cimss.ssec.wisc.edu/goes/blog/archives/31559 (accessed 2019-09-26).

27. Camera image stabilisation

Cameras are devices for capturing photographic images. A camera is basically a box with an opening in one wall that lets light enter the box and form an image on the opposite wall. The earliest such “cameras” were what are now known as camera obscuras, which are closed rooms with a small hole in one wall. The name “camera obscura” comes from Latin: “camera” meaning “room” and “obscura” meaning “dark”. (Which is incidentally why in English “camera” refers to a photographic device, while in Italian “camera” means a room.)

A camera obscura works on the principle that light travels in straight lines. How it forms an image is easiest to see with reference to a diagram:

Diagram illustrating the principle of a camera obscura. (Public domain image from Wikimedia Commons.)

In the diagram, the room on the right is enclosed and light can only enter through the hole C. Light from the head region A of a person standing outside enters the hole C, travelling in a straight line, until it hits the far wall of the room near the floor. Light from the person’s feet B travels through the hole C and ends up hitting the far wall near the ceiling. Light from the person’s torso D hits the far wall somewhere in between. We can see that all of the light from the person that enters through the hole C ends up projected on the far wall in such a way that it creates an image of the person, upside down. The image is faint, so the room needs to be dark in order to see it.

If you have a modern photographic camera, you can expose it for a long time to capture a photo of the faint projected image inside the room (which is upside down).

A room turned into a camera obscura, at the Camden Arts Centre, London. (Creative Commons Attribution 2.0 image by Flickr user Kevan, from Flickr.)

The hole in the wall needs to be small to keep the image reasonably sharp. If the hole is large, the rays of light from a single point in the scene outside project to multiple points on the far wall, making the image blurry – the larger the hole, the brighter the image, but blurrier it is. You can overcome this by placing a lens in the hole, which focuses the incoming light back down to a sharper focus on the wall.

Camera obscura using a lens to focus the incoming light for a brighter, sharper image. (Creative Commons Attribution 2.0 image by Flickr user Willi Winzig, from Flickr.)

A photographic camera is essentially a small, portable camera obscura, using a lens to focus an image of the outside world onto the inside of the back of the camera. The critical difference is that where the image forms on the back wall, there is some sort of light-sensitive device that records the pattern of light, shadow, and colour. The first cameras used light-sensitive chemicals, coated onto a flat surface. The light causes chemical reactions that change physical properties of the chemicals, such as hardness or colour. Various processes can then be used to convert the chemically coated surface into an image, that more or less resembles the scene that was projected into the camera. Modern chemical photography uses film as the chemical support medium, but glass was popular in the past and is still used for specialty purposes today.

More recently, photographic film has been largely displaced by digital electronic light sensors. Sensor manufacturers make silicon chips that contain millions of tiny individual light sensors arranged in a rectangular grid pattern. Each one records the amount of light that hits it, and that information is recorded as one pixel in a digital image file – the file holding millions of pixels that encode the image.

Cross section of a modern camera, showing the light path through the lens to the digital image sensor. In this camera, a partially silvered fixed mirror reflects a fraction of the light to a dedicated autofocus sensor, and the viewfinder is electronic (this is not a single-lens reflex (SLR) design). (Photo by me.)

One important parameter in photography is the exposure time (also known as “shutter speed”). The hole where the light enters is covered by a shutter, which opens when you press the camera button, and closes a little bit later, the amount of time controlled by the camera settings. The longer you leave open the shutter, the more light can be collected and the brighter the resulting image is. In bright sunlight you might only need to expose the camera for a thousandth of a second or less. In dimmer conditions, such as indoors, or at night, you need to leave the shutter open for longer, sometimes up to several seconds to make a satisfactory image.

A problem is that people are not good at holding a camera still for more than a fraction of a second. Our hands shake by small amounts which, while insignificant for most things, are large enough to cause a long exposure photograph to be blurry because the camera points in slightly different directions during the exposure. Photographers use a rule of thumb to determine the longest shutter speed that can safely be used: For a standard 35 mm SLR camera, take the reciprocal of the focal length of the lens in millimetres, and that is the longest usable shutter speed for hand-held photography. For example, when shooting with a 50 mm lens, your exposure should be 1/50 second or less to avoid blur caused by hand shake. Longer exposures will tend to be blurry.

Camera shake

A photo I took with a long exposure (0.3 seconds) on a (stationary) train. Besides the movement of the people, the background is also blurred by the shaking of my hands; the signs above the door are blurred to illegibility.

The traditional solution has been to use a tripod to hold the camera still while taking a photo, but most people don’t want to carry around a tripod. Since the mid-1990s, another solution has become available: image stabilisation. Image stabilisation uses technology to mitigate or undo the effects of hand shake during image capture. There are two types of image stabilisation:

1. Optical image stabilisation was the first type invented. The basic principle is to move certain optical components of the camera to compensate for the shaking of the camera body, maintaining the image on the same location on the sensor. Gyroscopes are used to measure the tilting of the camera body caused by hand shake, and servo motors physically move the lens elements or the image sensor (or both) to compensate. The motions are very small, but crucial, because the size of a pixel on a modern camera sensor is only a few micrometres, so if the image moves more than a few micrometres it will become blurry.

Optically image stabilised photo of a dim lighthouse interior. The exposure is 0.5 seconds, even longer than the previous photo, but the image stabilisation system mitigates the effects of hand shake, and details in the photo remain relatively unblurred. (Photo by me.)

2. Digital image stabilisation is a newer technology, which relies on image processing, rather than moving physical components in the camera. Digital image processing can go some way to remove the blur from an image, but this is never a perfect process because blurring loses some of the information irretrievably. Another approach is to capture multiple shorter exposure images and combine them after exposure. This produces a composite longer exposure, but each sub-image can be shifted slightly to compensate for any motion of the camera before adding them together. Although digital image stabilisation is fascinating, for this article we are actually concerned with optical image stabilisation, so I’ll say no more about digital.

Early optical image stabilisation hardware could stabilise an image by about 2 to 3 stops of exposure. A “stop” is a term referring to an increase or decrease in exposure by a factor of 2. With 3 stops of image stabilisation, you can safely increase your exposure by a factor of 2³ = 8. So if using a 50 mm lens, rather than need an exposure of 1/50 second or less, you can get away with about 1/6 second or less, a significant improvement.

Image stabilisation system diagram

Optical image stabilisation system diagram from a US patent by Canon. The symbols p and y refer to pitch and yaw, which are rotations as defined by the axes shown at 61. 63p and 63y are pitch and yaw sensors (i.e. gyroscopes), which send signals to electronics (65p and 65y) to control actuator motors (67p and 67y) to move the lens element 5, in order to keep the image steady on the sensor 69. 68p and 68y are position feedback sensors. (Figure reproduced from [1].)

Newer technology has improved optical image stabilisation to about 6.5 stops. This gives a factor of 2^6.5 = 91 times improvement, so that 1/50 second exposure can now be stretched to almost 2 seconds without blurring. Will we soon see further improvements giving even more stops of optical stabilisation?

Interestingly, the answer is no. At least not without a fundamentally different technology. According to an interview with Setsuya Kataoka, Deputy Division Manager of the Imaging Product Development Division of Olympus Corporation, 6.5 stops is the theoretical upper limit of gyroscope-based optical image stabilisation. Why? In his words[2]:

6.5 stops is actually a theoretical limitation at the moment due to rotation of the earth interfering with gyro sensors.

Wait, what?

This is a professional camera engineer, saying that it’s not possible to further improve camera image stabilisation technology because of the rotation of the Earth. Let’s examine why that might be.

As calculated above, when we’re in the realm of 6.5 stops of image stabilisation, a typical exposure is going to be of the order of a second or so. The gyroscopes inside the camera are attempting to keep the camera’s optical system effectively stationary, compensating for the photographer’s shaky hands. However, in one second the Earth rotates by an angle of 0.0042° (equal to 360° divided by the sidereal rotation period of the Earth, 86164 seconds). And gyroscopes hold their position in an inertial frame, not in the rotating frame of the Earth. So if the camera is optically locked to the angle of the gyroscope at the start of the exposure, one second later it will be out by an angle of 0.0042°. So what?

Well, a typical digital camera sensor contains pixels of the order of 5 μm across. With a focal length of 50 mm, a pixel subtends an angle of 5/50000×(180/π) = 0.006°. That’s very close to the same angle. In fact if we change to a focal length of 70 mm (roughly the border between a standard and telephoto lens, so very reasonable for consumer cameras), the angles come out virtually the same.

What this means is that if we take a 1 second exposure with a 70 mm lens (or a 2 second exposure with a 35 mm lens, and so on), with an optically stabilised camera system that perfectly locks onto a gyroscopic stabilisation system, the rotation of the Earth will cause the image to drift by a full pixel on the image sensor. In other words, the image will become blurred. This theoretical limit to the performance of optical image stabilisation, as conceded by professional camera engineers, demonstrates that the Earth is rotating once per day.

To tie this in to our theme of comparing to a flat Earth, I’ll concede that this current limitation would also occur if the flat Earth rotated once per day. However, the majority of flat Earth models deny that the Earth rotates, preferring the cycle of day and night to be generated by the motion of a relatively small, near sun. The current engineering limitations of camera optical image stabilisation rule out the non-rotating flat Earth model.

You could in theory compensate for the angular error caused by Earth rotation, but to do that you’d need to know which direction your camera was pointing relative to the Earth’s rotation axis. Photographers hold their cameras in all sorts of orientations, so you can’t assume this; you need to know both the direction of gravity relative to the camera, and your latitude. There are devices which measure these (accelerometers and GPS), so maybe some day soon camera engineers will include data from these to further improve image stabilisation. At that point, the technology will rely on the fact that the Earth is spherical – because the orientation of gravity relative to the rotation axis changes with latitude, whereas on a rotating flat Earth gravity is always at a constant angle to the rotation axis (parallel to it in the simple case of the flat Earth spinning like a CD).

And the fact that your future camera can perform 7+ stops of image stabilisation will depend on the fact that the Earth is a globe.

References:

[1] Toyoda, Y. “Image stabilizer”. US Patent 6064827, filed 1998-05-12, granted 2000-05-16. https://pdfpiw.uspto.gov/.piw?docid=06064827

[2] Westlake, Andy. “Exclusive interview: Setsuya Kataoka of Olympus”. Amateur Photographer, 2016. https://www.amateurphotographer.co.uk/latest/photo-news/exclusive-interview-setsuya-kataoka-olympus-95731 (accessed 2019-09-18).

Share this:

Share this: